[図4-7]第二紙(一)
第二の定理(ケイルによる)
軌道上のある場所での物体の速さとそこでの中心からの距離を半径として円軌道を描く物体の速さの比は、垂線×接円半径の平方根と中心からの距離の比に等しい。{点Aでの
物体の速さをvA、円軌道物体の速さをvOとすると、vA:vO=√SP・AR:SA}
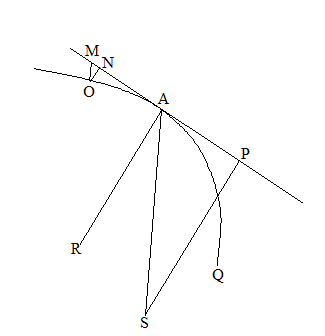
点Aでの物体の速さをvAとし、また、そこでの求心力で、そこでの中心までの距離を半径として円軌道を描くような速さをvOとする。前の定理に見るように、求心力はSAに比例し、ARを半径とする接円の無限小弧をvAで描く近心力(近R心力)はSPに比例する。
円運動の求心力(または遠心力)は、軌道半径(直径でも比例関係は同じ)で速さの2乗を割ったものに比例する。「円軌道運動第2段」で述べたとおりである。ゆえに、近R心力SP:求心力SA=vA2/AR:vO2/SA。
◇忠雄が言うに、vO2/SAは、SAを半径として円軌道を描く求心力である。A点での求心力なので、曲線軌道の物体に働く求心力と同じである。ゆえに、それと接円の近心力との比は、SA:SPに等しくなる。また、接円上での速さは、曲線上での速さと同じである。◆
ゆえに、SP・AR:SA2=vA2:vO2 。
◇忠雄が言うに、右辺のそれぞれの分母を取り去って左辺のそれぞれに掛けたものである。分母を取り去るのはかけ算をすることと同じである。◆
ゆえに、vA:vO=√SP・AR:SA。
第三の定理
楕円の正脇点における接円の半径は、(半長径)2/(半短径)である。
楕円は上編でも述べたように、長い円柱を斜めに切った断面の形である。和算家は「側円」と呼んでいる。「暦算全書」には「楕円」とある。
・[図4-8]による説明
[図4-8]第二紙(二)
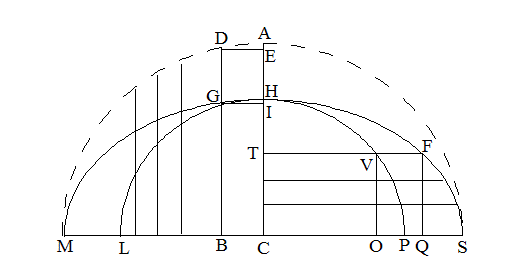
Cは楕円心である。MSは長径である。半長径をaとする(CS=a)。CHは半短径(=b)である。これの内と外に2つの円を描き、内側の小さい円は楕円の短径と同じ直径を持ち、外側の大きい円は楕円の長径と同じ直径を持つとする。中心はいずれも点Cとする。
横向きの軸に平行な直線上における、TV:TF (Vは小さい円周上、Fは楕円周上)と、縦向きの軸に平行な直線上における、BG:BD (Gは楕円周上、Dは大きい円周上)は、いずれも短径と長径の比になっている。ゆえに、OP:QSも IH:EAも同じ比になっている。TV:TF=BG:BD=OP:QS=IH:EA=b:a。
Hは正脇点である。AD、HGともに無限小弧であるとする。だからその弦の長さと同じとしてよい。また、矢であるEAとIHは無限小の2乗である。ゆえにこれらは弧の長さに比べても無限小である。無限小同士で比例関係があって、IH:EA=b:a、これはすでに上に出た。
ED=IG。矢は無限小の2乗なので、弧AD=弧HG。これは、弧と正弦の長さが等しくて、矢の長さが違うものである。
矢で弦の長さの2乗あるいは円弧の長さの2乗を割ると直径が得られることは、すでに「円軌道運動第2段のための定理」で述べた通りである。ゆえに、弧ADの接円の直径をdA、弧HGの接円の直径をdHとして、
dA:dH=AD2/(2a):HG2/(2b)=1/2a:1/2b=2b:2a。
◇前に言ったように、2つの矢の比がb:aであったから上のようになる。そして、2つの接円の直径は矢の長さに反比例する。また、二つの弧の長さは等しいから、そこは
1:1に置き換えることができる。◆
よって、dA:dH=2b:2a=b:a。
そして、dA=2aである。これは大きい円の直径であり、楕円の長径である。その半径は半長径aである。ゆえに、a:dH/2=b:a。ゆえに、正脇点での接円半径dH/2は、a2/bである。
同様に、点Mあるいは点Sにおける接円の半径は、b2/aである。また、CH:CAもBG:BDも、縦線の区間の楕円と大きい円の比例はどこでもb:aである。ゆえに、楕円の全面積S(楕円)と大きな円の全面積S(大円)の比は、b:aである。また、TV:TFのような横線にも同様の比例関係があるので、小さな円と楕円の面積比もb:aである。
面積のあいだの比は、S(楕円):S(大円)=S(小円):S(楕円)=b:a。
第四の定理
楕円軌道を運行する物体の正脇点における速さと、その半長径(これは正脇点から中心=焦点までの距離に等しい。上編下巻で述べた)を半径として円軌道を描くのに要する速さは等しい。
第二の定理によると、vA:vO=√SP・AR:SA ([図4-7]における)であった。 楕円の正脇点の接線に対する垂線(SP)は半短径bに等しい。また、第三の定理を見ると、正脇点の接円の半径(AR)はa2/bである。よって、SP・AR=a2となるので、√SP・ARは半長径aになる。また、そこから中心までの距離SAも半長径に等しい。よって、楕円の正脇点における速さvH とその点での円軌道の速さvC の比はa:aであるから、つまり両者は等しい。 vH=vC 。速さが同じだといっても、その向きが違うので、結果的に描かれる曲線は種々の違いをなすのである。
第五の定理
・[図4-9]による説明
[図4-9]第二紙(三)
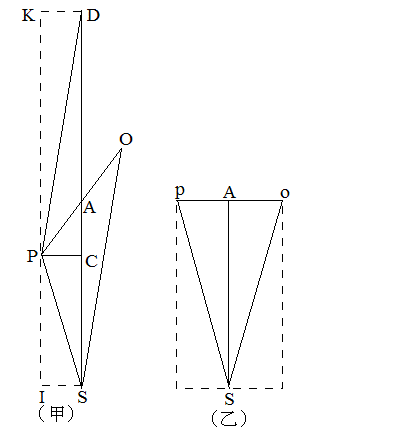
今、面積S(甲)を持つ△SPOと、面積S(乙)を持つ△Spoがあるとする。POとpoは長さが等しい。PO=po。それぞれの中点をともにAとし、SAは両図形で共通であるとする。po⊥SAで、POはSAに対して傾いているとする。この時、S(甲):S(乙)=垂線PC:PA。(または、=PC:AO)
甲の図でSAを延長して、SA=ADとなる点Dをとる。AO=AP。対頂角∠OAS=∠PAD、かつAS=ADなので、△PAD≡△OAS。ゆえにS(甲)=S(△PDS)。
直線SD=2ASに、それに下ろした垂線PCの長さを掛けると長方形SIKDの面積となる。その半分はS(△PDS)=S(甲)である。よって、S(甲)=SA・PCである。また、乙の図でSAにpA(またはAo)、または、それと同じ長さである甲の図のPA(またはAO)を掛けると、S(乙)になる。
ゆえに、S(甲):S(乙)=垂線PC:AO(または、PC:PA)。
◇上の甲、乙の名前は順序によって名付けたものなので、面積の大小の順序にはよらない。◆
第六の定理
・[図4-10]による説明
[図4-10]第二紙(四)
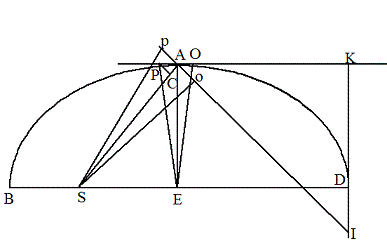
楕円軌道を運行する物体の正脇点での速さと同じ速さで、中心に対して直角の方向に運動する物体があるならば、2物体が同じ時間に描く面積の比は、楕円の短径と長径の比に等しい。{それぞれの面積速度をw(楕)、w(円)として、w(楕):w(円)=2b:2a}
BADは楕円である。Sは焦点であり、求心力の中心である。KIは正脇点での接線AKに垂直である。POとpoは、どちらも、正脇点の前後にある無限小の線分である。(無限小の弧も無限小の線分も同じことである) PO=poとする。
たとえば、甲と乙の二つの物体があって、どちらも正脇点を通って同じ速さで、甲はPOを運行し、乙はpoを運行する。2つの三角形の面積のあいだの比例関係は、甲の描く面積S(△OSP):乙の描く面積S(△oSp)=w(楕):w(円)=AK:AI。その理由は、この図の△SPOと[図4-9]の甲は同じであり、この図の△Spoと[図4-9]の乙は同じであり、w(楕):w(円)=S(甲):S(乙)=PC:PA。この比は、AK:AIと同じである。これが、無限小の線分を運行する二物体の速さが等しくて向きが違う場合の面積速度の比例関係である。
AK⊥AE。AI⊥AS。ゆえに、AK:AI=AE:AS。AEは半短径であり、ASは半長径である。ゆえに、w(楕):w(円)=2b:2a =b:a。
上の定理によって、次の一致関係を得る。
楕円軌道運行の公転周期は、その半長径と等しい半径を持つ円軌道運行の公転周期に等しい。
・[図4-11]による説明
[図4-11]第二紙(五)
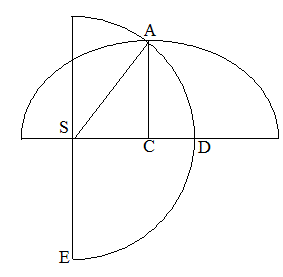
楕円の正脇点から焦点までの距離が半長径に等しいことは、もとより楕円形の幾何学的性質である。上編下巻にある通りである。
第四の定理によると、正脇点での速さ vH と 半長経ASを半径としてADEの円軌道を描く速さ vC とは等しい。また、第六の定理により、楕円軌道の正脇点での無限小時間において描かれる面積(面積速度)の比には、w(楕):w(円)=b:a が成り立つ。前節を思い出すと、運行時間は面積に比例するので、周期の比例関係は、面積速度で全面積を割った値の比になる。そして、第三の定理を見ると、全面積の比例関係は、S(楕円):S(大きい円)=b:a となっている。ここで、大きい円は楕円の半長径を半径とする円である。
ゆえに、(楕円軌道運行の周期):(円軌道運行の周期)=b/b:a/a=1:1 となる。つまり、両者は等しい。
◇忠雄が言うに、第一の定理と第二の定理は、ケイルが述べたものである。残りは、ケイルに基づいて私が述べたものである。◆
この理由で、半長径を平均距離とし、衆動一貫の法則を用いた計算をする時にもこの距離を用いる。これは上編下巻に述べたことである。ある人は半長径と半短径を掛けて平方根をとったものを平均とするかもしれないが、それは違うものである。それは、楕円の面積と等しい面積を持つ円の半径である。
11.衆動一貫の法則の起源〔ケプラーの第3法則の証明〕(中編下巻「衆動一貫比例起源」より)
2つの物体がそれぞれ違う半径の円軌道を回っているとする。その求心力が中心からの距離(つまり軌道半径)の2乗に反比例している場合は、距離の3乗と周期の2乗は比例する。
◇求心力が中心からの距離の2乗に反比例することは「重力」の節で述べた。また、円軌道運動では、求心力も遠心力とは常に同じ大きさであるので、求心力と言っても遠心力と言っても同じことである。しかし、自由運動においてはつねに求心力という。前にも言った通りである。◆
・[図4-13]の説明
[図4-13] 第三紙(二)
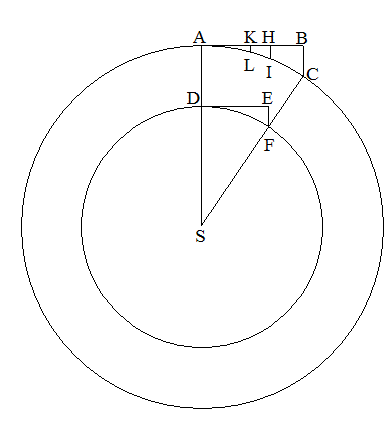
大小2つの円軌道があるとする。そして、それらの軌道の直径を、それぞれ、d2=2AS、d1=2DS とする。それぞれに、無限小の円弧、ACとDFをとる。2つの弧の中心角は等しい。∠ASC=∠DSF。 すると、AC:DF=d2:d1 。 また、
AC:AI=d2:d1となるように弦AIを設ける。ゆえに、AI=DF。
矢の長さは弦の長さの2乗に比例する。「円軌道運動第2段のための定理」で述べた通りである。ゆえに、BC:HI = AC2:AI2=d22:d12 が成り立つ。(HはIからABに下ろした垂線の足)
また、BC:EF= d2:d1=d22:d2d1 が成り立つことから、HI:EF=d12:d2d1=d1:d2となる。
さらに、HI:KL = d2:d1となるようなABへの垂線KLをとると、KL:EF=d1:d22/d1=d12:d22 である。ここで、KLとEFは、それぞれお互いの円軌道の半径の2乗(2物体の中心からの距離の2乗)に比例している。つまり自身の軌道半径については反比例している。ゆえに、KLとEFを2物体のそれぞれの円軌道における求心力と見なせる。それで、ALとDFは、それぞれの物体が同時間に運行する区間であることがわかる。矢の長さは弧の長さの2乗に比例し、弧の長さは矢の長さの平方根に比例するから、AL:AI=√KL:√HI。そして、前に出た通り、KL:HI=d1:d2。だから、AL:AI=√d1:√d2。
ALとDFは、それぞれが同じ時間に運行する距離であって、DF=AI。(前に出た通りである)ALは外側の円軌道の物体の速さ(v2とする)に対応し、AIは内側の円軌道の物体の速さ(v1とする)に対応する。だから、v1:v2 =√d1:√d2。同じ距離を運行するのに要する時間は速さに反比例するから、物体がAからIまで動くのに要する時間を
t(A→I)、DからFまで動くのに要する時間をt(D→F)で表すと、
t(A→I):t(D→F)=√d2:√d1。 AI=DFだから、周期の比は、内側の物体の周期をP1、外側の物体の周期をP2とすると、
P2:P1 = t(A→I)(πd2):t(D→F)(πd1) =t(A→I)d2:t(D→F)d1。{πは円周率}
t(A→I):t(D→F)=√d2:√d1 であったから、ゆえに、
P2:P1 = d2√d2:d1√d1。
これから、P22:P12 =d23:d13。または、周期の2乗の比は、半径の3乗、すなわち、物体の中心からの距離の3乗の比と同じである。
このことから、太陽系の諸惑星はすべて太陽の力で軌道を回っていることがわかる。この理由によって、太陽は宇宙の支配者であるといえる。
◇上の2つの円軌道の距離と周期の関係は、もともとはケプラーが発見したものであるが、それが成り立つ数理は、ニュートンによって初めて明らかになった。上の証明は、忠雄がホイヘンスに倣って考えて述べたものである。諸惑星の軌道は楕円形なのでその中心までの距離は一定ではないが、一貫の法則に適用するにはその最大と最小の平均を取る。そのことは「円軌道と楕円軌道における周期の一致」で述べた通りである。また、楕円曲線の数理の詳しいことは下巻で述べる。◆
以上で、「日本の古典で学ぶ天文学」と題した志筑忠雄『暦象新書』の現代語訳でのケプラーの3法則に関する証明を完結する。日本初の物理学の
教科書とも言える本書が、ケプラーの3法則の証明が詳細に議論されるほど高度なものであったことは、驚嘆に値する。
(完)
--------------------------------------------------------
付録:原典資料紹介(その4)