日本の古典で学ぶ天文学(第1回)
原著 J. Keill, 蘭語訳 J.Lulofs
翻案著者 志筑忠雄、現代語訳・監修 上原貞治
緒言
今回、「日本の古典で学ぶ天文学」と題し、江戸時代の日本語の文献をテキストとして、天文学と物理学のもっとも重要な基礎の一つである「ケプラーの惑星運動」の法則からの「ニュートンの万有引力の法則」を導出の数学的な解説を載せることにした。具体的には、観測事実であるケプラーの第1,第2法則から、ニュートンの重力の逆2乗則を導く計算が説明される。現在の学校で習う物理学では、この証明は微分方程式を用いたかなり高度なものになり、高校の数学と物理学のレベルを超えている。おそらくは、天文学か物理学を専攻する大学1年生のレベルになると思われる。しかし、ここに載せる計算は、中学生でも理解できるはずのものである。それは、図形の比例計算くらいしか用いていないからである。微分が微小角度の作図のレベルに落とされているのである。また、中学理科とせいぜい高校の物理Iの力学の知識があれば、物理の内容を含めてすべて理解することも可能であろう。
現代人で、ケプラーの第1,2法則からニュートンの万有引力の導出の計算をフォローしたことのある人はほとんどいないであろう。しかし、この連載を読めば、あなたは確実にそれをフォローすることができるであろう。数学的に厳密な証明かどうかは問題があるが、天文学においては現象と筋道を理解し体感することがまず重要であり、その目標は達成できるものと信じる。
解題
ここで用いるテキストは、志筑忠雄(しづきただお、1760-1806)の『暦象新書』(*1)の関連する部分である。『暦象新書』は、江戸時代の1798〜1802年に上中下の3編に分けて書き上げられた日本で最初の物理学の教科書と呼ぶべき本である。この本は、また、日本で初めて書かれた近代天文学の本格的な解説書でもあり、そこにはニュートン物理学の計算まで書かれている。内容には、著者でのオランダ語翻訳家の志筑のオリジナルの部分もあるが、ここで取り上げたのはおもに、志筑が元本として用いたJ. Keill(英国人Jl, 1671-1721)の原著(*2)(ラテン語)にある部分である。ただし、志筑が直接利用したのはそのオランダ語訳本(*3)(J. Lulofs訳)である。志筑は、長崎在住の元オランダ語通詞であった。
この元本のラテン語原著およびその英訳本、蘭語訳本は、いずれもインターネット上で参照可能であるが、ここでは、志筑の翻案のみを用いた。志筑は、計算も含めて天文学の内容を完全に把握できているので、原著に戻る必要はなかった。独力で、この計算を理解した志筑忠雄は間違いなく日本の江戸時代の誇る天才である。ただし、『暦象新書』は、漢字カナ混じりの文語体で、特に数式に対応する部分は漢文で記述されている。それを読みながら計算をフォローすることは現代人には困難なことなので、筆者(上原)はその現代語訳を作り、現代の形の数式に翻訳することにした。これが、Keill原著の数式に戻っているかどうかは確認していないが、大勢においては戻っているはずである。
凡例
以下の内容は、『暦象新書』から抜粋した部分の現代語訳である。節番号は、この目的の解説記事のために振り直したもので、『暦象新書』における掲載とは順番が異なっている場合が多い。括弧内に『暦象新書』の出典場所を記す。図版番号も上原が志筑の翻案書の巻ごとに適当に順番に振ったものである。また、これは翻案書の抜粋であるので、参照されている箇所で本連載に引用のない部分があるが、適宜、現代の中学理科・高校物理の教科書や一般の天文学解説書に記述があると思うので、それらを参照していただきたい。
ここで、筆者がした仕事はほぼ現代語訳と数式の変換に尽きる。ただし( )内と[ ]内は筆者による注で、( )内は筆者が志筑の記述のわかりにくい部分を補足したもの、[ ]内は(志筑の知らなかった)現代の科学の観点からみた注釈である。一方、元本のテキストでは、志筑が挿入した解説の部分に、連続する行の「一字下げ」を用いている。現代語訳では、横書きにしたこともあって、このような一字下げを採用しなかった。その代わりに、その部分の始めと終わりにそれぞれ◇と◆のマークを入れて、志筑が一字下げを行った部分を示した。ただし、一字下げをしていない部分でも志筑の見解がおもになっている場合も多いので、これについてはあまり拘泥しない方が無難であろう。
図の説明や図を使った定理の証明において、例えば、直線AB、円弧ACなどに添えるべき直線、線分、円弧およびその長さなどを区別する記号は、htmlでは煩わしいので省略した。図や説明によって区別していただけるものと信ずる。
連載は、3〜4回にわたる予定である。全体の流れは、最後に明らかになるが、おおむね、中心力(求心力)による運動の一般論とケプラーの第2法則の説明(今号(第1回)の内容)、楕円の基本的な性質、と進み、最後にケプラーの第1法則の楕円軌道からニュートンの万有引力の距離の逆2乗則が導かれる。各回においては、図を使って計算を自分で確認しながら各式のチェックを進めていってほしい。どれも、見た目ほどの難しさはない計算である。
(*1) 志筑忠雄「暦象新書」(1798-1802) 文明源流叢書第2巻、国書刊行会編 (1914).(早稲田大学古典籍総合データベース)
(*2) J. Keill "Introductio ad veram physicam et veram astronomiam" (1725)
(*3) J. Lulofs(訳) "Inleidinge tot de waare natuur- en sterrekunde, of de natuur- en sterrekundige lessen"(1741)
志筑忠雄「暦象新書」現代語訳(抄)−ケプラーの第1、第2法則の証明に関する部分
1.惑星軌道の三角形面積比例法則の起源〔ケプラーの第2法則の証明〕(中編下巻「星行応三角積起源」より)
◇諸惑星の運行において、軌道上の前後2点と太陽の3点を結んでつくる形の面積にその運行に要する時間が比例することは、すでに上編下巻で述べた。ここでは、それが生じる原理について説明するものである。◆
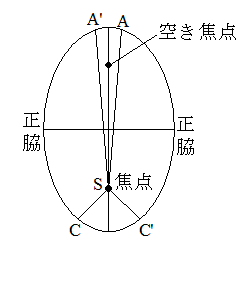
・[図4-3]による説明
[図4-3]第一紙(二)
両脇の2点を「正脇」という。中心でないほうの 焦点を「空き焦点」という。中心を楕円心と呼ぶ。
たとえば、AからA'まで運行する時間とCからC'まで運行する時間が等しいときは、ASA'の面積とCSC'の面積は等しい。
定理(速さの比例)
一般に、求心力によって自由運動をして曲線の軌道を描く物体の速さは、軌道上のその点での接線に中心から下ろした垂線の長さに反比例する。(自由運動には振り糸を使って力を支えるようなものを含まない。また、曲線は自由落下の直線運動を含まない。)
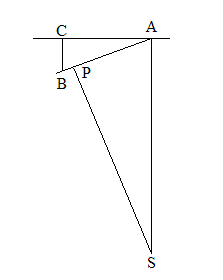
・[図4-4]による説明
[図4-4]第一紙(三)
SA⊥AC。 SP⊥AB。
Sは求心力の中心である。(地球においては、地球の中心である)物体がAからCに向かって運動している。ACはASに比べると無限小であるとする。ゆえに重力(もしくは求心力。どちらでも同じ意味である)の向きとASの方向は平行である。物体は、無限小時間にACを進む間に重力のために向きが変わってBに到達するので、ACであった速度がABになる。だから、(A点での速さ):(B点での速さ)=AC:AB。「力を加えると速度が変わる」の節で詳細に述べた通りである。
SA⊥ACであるとし、SからABに下ろした垂線の足をPとする。このとき、
SP:SA=AC:AB。ゆえに、(A点での速さ):(B点での速さ)=垂線SP:垂線SA。速さが大きい時は垂線は短く、速さが小さい時は垂線は長い。だから、速さがその点に関する垂線の長さに反比例することがわかる。
◇無限小の直線であるABのようなものが、無限大個積み重なって、ひとつの円や楕円のような軌跡ができる理屈については、「等速円運動」の節で述べた。◆
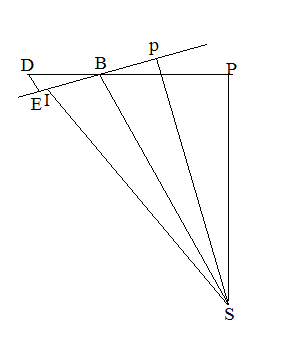
・[図4-5]による説明
[図4-5]第一紙(四)
IとEが同じ点である場合は円軌道である。点IがEの右にある場合は、物体は上昇していて減速中である。この図もそうである。左にある時は、下降していて加速中である。
BD、EDどちらも無限小の線分である。物体がBからDに行く間に落ちて、Eに到達する。その時、(点Bでの速さ):(点Eでの速さ)=BD:BE である。BEは無限小なので、SB//DEである。また、∠DBE=∠BSIとなるように、線分SIを引く。 この時、SB//EDだから、∠SBI=∠BED。ゆえに、△BED∽△SIB。ゆえに、
(B点での速さ):(E点での速さ)=BD:BE=SI:SB。
Sから直線BDとBEのそれぞれに下ろした垂線の足を、それぞれPとpとする。
∠BSI=∠EBD=∠PSp。ゆえに、∠PSB=∠pSI。ゆえに、△PSB∽△pSI(どちらも直角三角形)。ゆえに、SI:SB=pS:PS。
前に出たように、(B点での速さ):(E点での速さ)=SI:SB。ゆえに、
(点Bでの速さ):(点Eでの速さ)=垂線pS:垂線PS。
どの点の速さの比例関係もすべて同様である。このように、各点での速さはすべてその垂線の長さの逆数に比例することがわかる。だから、各点での速さを知りたい時は、その点での接線に垂直な線の中心からの長さを求めて、それの逆数を得ればよい。
上の比例関係については、たとえ求心力が一定であっても、または、距離に応じて強くなっても弱くなっても、あるいは距離の3乗、5乗、6乗のべきに比例して強くなったり弱くなったりしても、また円軌道であっても楕円軌道であっても、その他種々の軌道を描くとしても、速さの比例関係はこのようになる。
◇ただし、これは、一つの物体が一つの軌道内で運行している内部での比例関係である。二つの物体がそれぞれの軌道にある場合には、それぞれ別々の比例になる。また、求心力のすべてが物体に掛かる場合の比例関係である。振り子の運動のように、糸で支えて求心力のかかり方を分けたり加えたりする場合は、また別の比例関係になる。◆
以上を定理として、問題の法則の起源を証明する。
面積比例法則の起源
すべて、自由運動で曲線軌道を描く物体においては、所要時間と三角形面積は比例する。
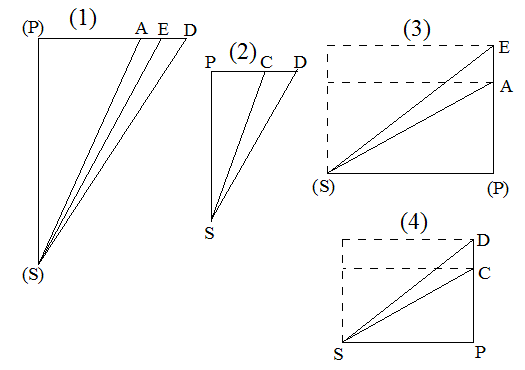
・[図4-6]による説明
[図4-6]
図(1)で、AE、EDはいずれも無限小の線分あるいは無限小の軌道の弧である。(S)(P)は、軌道の接線に対する垂線である。物体はある時間にAEを運行し、次の同じ長さの時間にEDを運行する。
垂線の長さが同じであるならば、中心からの距離がA(S)であってもE(S)であっても、AE=EDである。同じ時間を要する運行の面積であるA(S)EとE(S)Dとは等しい。
垂線の長さが違う場合を考える。一つの軌道上の別の場所に無限小の2区間、AEとCDをとる。図(2)、(4)でCDへの垂線SPをAEでの速さとし、図(3)でAEへの垂線(S)(P)をCDでの速さとする。逆数の比例はお互いの相手に比例することになるからである。 この時、同じ時間での運行について、AE:CD=SP:(S)(P)。ゆえに、
AE・(S)(P)=CD・SP。この式の両辺を三角形の面積をS(△)で表すと、2S(△A(S)E)=2S(△CSD)。よって、ゆえに、同じ時間の運行について、△A(S)Eの面積と△CSDの面積が等しいことがわかった。
楕円軌道全周において、どの2点を取って比べてみても同じ比例関係が成り立っている。楕円だけでなく、一般の中心力による自由運動の曲線軌道については、同じ法則が成り立っている。
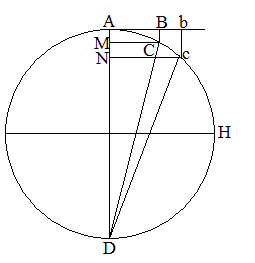
2.円軌道運動第2段のための定理 (中編上巻「旋輪体動法」より)
・[図3-12]による説明
[図3-12]第二紙(四)
例えば、ACDの円軌道で、BCとbcの2線分がどちらも無限小であるとき、それらの長さの比率に BC:bc=AC2:Ac2 が成立する。
ACとAcはどちらも無限小の円弧である。だから、どちらもそれぞれの弦(線分ACと線分Acの長さ)と差がない。(弦というのは、たとえば、線分AHが円弧ACHの弦である、ということから類推しなさい)それは、円弧が無限小なので線分と差がないからである。また、BCとbcは、どちらも点Aでの接線Abに垂直である。ADは円軌道の直径である。CM⊥AD、cN⊥ADである。また、∠DHA、∠DcAのように円周上にあるどの点における角もすべて直角になる。(直角とは90°のことである)だから三角形ACDは直角三角形でCMはその直角から斜辺に下ろした垂線である。直角三角形AcDにおいては、cNがその直角から斜辺に下ろした垂線である。だから、直角三角形の辺の相似関係から
AD:AC=AC:AM
AD:Ac=Ac:AN だから、
AD・AM=AC2
AD・AN=Ac2 また、
AD・AM:AD・AN=AM:AN=BC:bc ゆえに
BC:bc=AC2:Ac2
たとえ無限小の円弧でなくても、その中心角が小さければ、上の数理からのはずれはわずかである。例えば、1分角の円弧では、円弧の長さと弦の長さの差は、円弧の長さの1/100未満である。
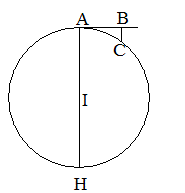
3.求心力一般論のための定理(下編上巻「求心常経張本」より)
第一の定理:円運動の求心力 (全1段)
・[図5-1]による説明
[図5-1]第一紙(一)
円軌道を運行する物体においては、求心力は (速さ)2/半径 に比例する。
ABは点Aでの接線である。ACは無限小の円弧(半径は有限で中心角が無限小)である。ここで、中編上巻の「円軌道運動第2段のための定理」を思い出すと、無限小の円弧に対しては、矢×直径=(円弧)2。また、速さは定まった時間に運行する無限小の円弧に比例し、求心力はその矢の長さに比例する。それで、BCは、速さACの2乗を直径AHまたは半径AIで割ったものに比例する。(これは、中編の「円軌道運動の法則」のところで詳しく述べた遠心力についての比例関係と同じである)
4.円軌道と楕円軌道における周期の一致のための定理 (中編下巻「正楕二円適等」より)
楕円軌道運行の公転周期は、その長径と等しい直径を持つ円軌道運行の公転周期に等しい。
第一の定理(ケイルによる)
曲線軌道を運行する物体の各点における求心力とその接円の近心力の比は、中心からの距離と垂線の長さ(物体がある点での軌道の接線に中心から下ろした垂線を指す)の比に等しい。
◇忠雄が言うに、円軌道においては、求心力と遠心力は常に大きさが等しい。その他の曲線については、遠心力はあることもあるが無いこともある。求心力は常にある。ゆえに、曲線上の運行を論じるときは、まず、求心力を取り上げる。また、「接円」というのは、たとえば、前に述べた「塵跡線の高さの2倍を半径とする円の円弧が塵跡線の最下部の弧に対応する」とするような円を指す。また、ここでいう物体とは、以前に述べたような自由運動をする物体のことである。◆
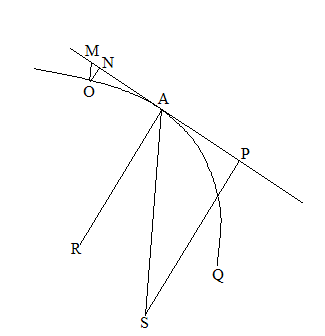
・[図4-7]による説明
[図4-7]第二紙(一)
QAOは曲線の軌道である。物体は、求心力によってこれを描く。点Sが中心である。AOは、無限小時間における運動である。MPは点Aにおける接線である。ARは、AOにおける接円の半径である。ゆえにこの接円の無限小の円弧と曲線弧AOは同一であると考えてよい。SPは中心Sから接線APに下ろした垂線である。OM//SA、ON//SPである。
物体が点Aにあるとき、求心力OMが働く。その際に、接線から遠ざかろうとする力の成分はONである。これを、接円の中心Rに近づこうとする「近心力」(近R心力)と解釈する。近R心力:求心力=ON:OM。また、∠MON=∠ASP。ゆえに、
(近R心力):(求心力)=垂線SP:中心からの距離SA。
(つづく)
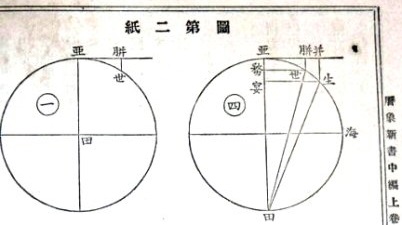
付録:原典資料紹介
志筑忠雄「暦象新書」(1798-1802) 文明源流叢書第2巻、国書刊行会編 (*1)より
「円軌道運動第2段のための定理(筆者現代語訳)」冒頭部対応部分(左)と円運動の説明図(右)
(*3) J. Lulofsオランダ語訳本"Inleidinge tot de waare natuur- en sterrekunde, of de natuur- en sterrekundige lessen”(グーグルブックス)より
「円軌道運動第2段のための定理」の証明部分と図。志筑はオランダ語訳本のこれらの部分を読んだ。
今号表紙に戻る