ホーマン軌道に関する計算(1)
~人工衛星の近地点と遠地点~
上原 貞治
今回から、2回にわたって、ホーマン軌道に関わる軌道の計算について述べる。ホーマン軌道は、人工衛星を低い軌道から高い軌道(たとえば静止軌道)に上げるための遷移軌道の一種で、燃料がもっとも節約できると言われている。しかし、ここでは、人工衛星の技術のことは問題にせず、単純に、ケプラー運動の楕円軌道に関係する数式計算を行う目的で使うことにする。この数式計算は、高校の物理Iと数学IIIくらいまでの範囲で手でできる計算である。現在の天文計算は、コンピュータでの数値計算万能かもしれないが、たまには手で数式の計算をしてみるのもいいだろう。簡単な計算で、楕円軌道について、いろいろ有用なことがわかる。
1. ホーマン軌道とは
ホーマン軌道は、人工衛星を(人工惑星でもよい)楕円軌道に投入する際、重力中心への方向に対して垂直の方向に速度を与えた場合の軌道のことをいう。地球を球体とすれば、人工衛星の速度ベクトルが地表と平行(水平)になればよい。この時、加速は短時間に行う。あるいは、加速が終わった時点で、衛星の速度ベクトルが地面に平行になっていたらよい。このような加速点は、結果的に、近地点あるいは遠地点となる。ケプラー運動の楕円軌道で、重力中心(地球中心)への方向と速度方向が垂直になるのは、近地点と遠地点だけである。便宜上、ここでは、速度が与えられる点を近地点とし、楕円軌道の正反対側の遠地点まで人工天体が向かうものとする。逆に、遠地点をスタートにして近地点に向かう場合もまったく同じ数式が使えるので、これにこだわることはない。今の場合、近地点距離(重力中心から測って)をq、そこでの速さをv(vは、qを測る方向に対して、直角方向とする)とする。これらを人が与えた変数とし、その場合、遠地点距離Qと遠地点での速さVはどうなるであろうか、とういうのが今日の問題である。
図1に遷移軌道としてのホーマン軌道、図2に変数の図解を示す。

図1:遷移軌道としてのホーマン軌道(②③④を結ぶ楕円軌道)
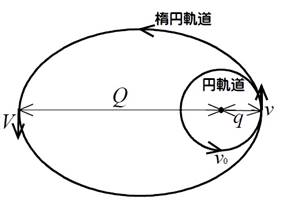
図2:楕円軌道における近日点距離、そこでの速度、遠日点距離、そこでの速度の定義の図示。
2. 連立方程式
重力のような中心力(1つの引力源まで距離に依って力の強さが決まる)の場合は、角運動量の保存則が成立する。角運動の保存則は、引力中心の周りの空間が回転対称(等方的=方向依存性がない)であることに対応している。近地点と遠地点の角運動量保存則を式にすると、
![]()
q と vの間に直角でない角度θがついている時は、mqv sinθ となる(その場合は、qは近地点距離にはならないが)。近地点、遠地点では、直角なのでsinθ=1である。もちろん、両辺にあるm(人工衛星の質量)は取り除いてよい。角運動量保存則は、ケプラーの第2法則である「面積速度の法則」と同等である。なお、面積速度は、一般に、(1/2)qv sinθである。
未知の変数が、QとVの2つあるので、もう1つ方程式を立てる。それには、エネルギー保存則を使う。人工衛星のエネルギーは、運動エネルギーと位置エネルギーの和で表される。たとえば、近地点で、運動エネルギーは、(1/2)mv2であり、位置エネルギーは、-GMm/q である。ここで、位置エネルギーは、人工衛星が地球から無限遠にある時が0になるように、基準が定められている。分母が距離の1乗になっているのが、引力が逆2乗則であることに対応する。エネルギーは、力を距離で積分したものになるからである。さらに、地球から離れるほど位置エネルギーは大きくなるので、マイナスの符号がつく。これから、もう一つの方程式が作られる。人工衛星の質量mは、両辺で約分されるので、不要である。
![]()
ここで、GMは、万有引力定数と地球質量の積である。ただ、この値は、数値的には見慣れないものかもしれないので、補助的な式を使って、別の変数 v0で表すことにする。ここで、v0は、近地点qにおいて、人工衛星を同様に地面に平行に打ち出したとして、軌道が結果的に円軌道になる場合の速度である。半径qの円軌道の人工衛星の周回速度と言い換えても良い。この時は、軌道上のどの点でも、引力(GMm/q2)と「遠心力」(mv02/q)が等しくなり、人工衛星は円軌道を描く。
![]()
これより、
![]()
これを(2)に代入して、
![]()
となる。(2’)と(1)を連立方程式とみて、Qを消去すると、Vについての2次方程式になる。2次方程式は、解の公式で解ける。ここで、楕円軌道においては、(2)の両辺が負である(つまり、人工衛星が地球周回軌道にトラップされていることは、人工衛星の全エネルギーが負であることを意味する)ことに留意する。従って、
![]()
という関係が要請される。これは、vに上限を与えるものである。vが(√2)v0に達するかあるいは越えると、人工衛星は脱出速度に達して地球周回軌道を巡らない。2次方程式を解くにあたって、解の公式に根号が出てきてその処理が必要になるが、(4)が成立していることを前提とする。これは、根号の中身が正という条件となる。
3. エネルギー保存則が成立することの確認
ここで、人工衛星の周回において、エネルギー保存則が成立していることを確認しておく。運動する人工衛星は、運動量保存則によって、地球をも揺さぶっているはずであって、それでは、地球が運動エネルギーを一部持ち逃げすることになるではないか、という疑問に答えるものである。
人工衛星が地球を揺さぶるという考えにもとづいて、地球と人工衛星の重心系を考えて、その系で運動量保存則が成り立つとする。考察のために、その運動量保存則を、象徴的に、
![]()
と書く。ここでMは地球質量、sは地球のだいたいの速度である。地球は衛星が加速されるまでは止まっていたとし、このs は速度の増分であると同時に、地球が人工衛星のために動き出した速度である。この時、人工衛星の運動エネルギーは、e=(1/2)mv2、地球における運動エネルギーは、E=(1/2)Ms2 であるとすると、地球が持ち去る運動エネルギーは、
![]()
となる。人工衛星の質量と地球の質量の比に比例して、人工衛星のエネルギーのごくごくわずかの部分が地球に持ち去られるにすぎないので、これは、完全に無視してよい。よって、人工衛星単体で、エネルギー保存則が極めて正確に成立する。
4. 連立方程式の解
(2’)と(1)を連立方程式とみて、Qを消去すると、Vについての2次方程式になる。これは、解の公式で解けるので、ここでは結果だけを示す。Vの解は、2つあって、
![]()
である。Qについての解とセットで示すと、
これで、方程式が解けた。2つの解のうちの1つめは、もとの方程式が近地点と遠地点で対称になっていることによる自明の解で、これは近地点の状況は近地点の状況に等しいという同義反復とみてもよいし、あるいは、軌道を1周すると、また同じ近地点に同じ速度で帰ってくると言っていると考えてもよい。遠地点として意味があるのは自明でないほうの解であって、それは、
![]()
である。
5. ケプラーの第3法則との関係
今回は、エネルギー保存則を用いて方程式を解いたが、ケプラーの第3法則を使ってもよいのではないかという考えが浮かぶだろう。たしかにそうだが、そちらはより複雑になりそうである。しかし、ここでは、ケプラーの第3法則が上の解から出てくることだけ簡単に説明しておこう。
ケプラーの第3法則は、中心天体を共通とする異なる周回軌道において、P2/a3 が一定であるという法則である。ここで、Pは公転周期、aは楕円軌道の平均半径(軌道長半径)である。軌道半径q、公転速度 v0の円軌道では、
![]()
なので、これから計算をすると
![]()
となる。円軌道の場合は、確かに、軌道半径によらないし、自然定数だけで決まっている比率になる。
今度は、前節で解として得られた楕円軌道を考えると、
![]()
である。公転周期は、楕円の面積を面積速度=qv/2で割ることによって得られる。楕円の面積は、abπ で、ここで、bは楕円の短半径である。楕円の短半径は、楕円の性質より、qとQの相乗平均
、
![]()
となる。長半径は相加平均、短半径は相乗平均である。
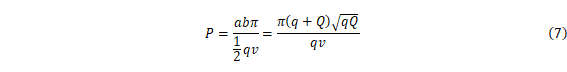
これら楕円軌道の場合のPとaの式に、Qとして(5’)の解を代入すると、やはり、楕円軌道でも、q, v, v0 に依存せずに、(6)とまったく同じ関係が成立していることがわかる。解はケプラーの第3法則を満たしている。
なお、楕円軌道のPの代入後の具体的なかたちを、次回に提示して利用する。次回は、これを太陽の周りの流星群の軌道の考察のために利用する予定である。
(つづく)