ホーマン 軌道に関する計算（２）

〜ペルセ ウス座流星群はなぜ毎年出現するのか〜

　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　上原　 貞治

 

前回の「ホーマン軌道に関する計算（１）」では、地球を周回する人工衛星について、近地点（引力中心からの距離をｑとする）での速度ｖ（方向は引力中心の方向と垂直）を与えた時の遠地点距離Ｑ、速度Ｖを計算する関係式を導いた。これは、計算練習のようなものであったが、今回は、これを、流星群において、母彗星からの流星物質の広がりについての議論に応用する。

 

５．近日点での速度と周期の関係

今回も、前回と同様に楕円軌道を考えるが、流星群の議論をする関係上、引力中心の天体を地球ではなく太陽とする。したがって、前回の議論の地球を太陽で置き換え、近地点、遠地点を、近日点、遠日点に置き換えるものとする。なお、前回、地球と人工衛星の２体しか問題にしなかったのと同様、今回もすべて、太陽と流星物質の２体問題のみを考え、地球や木星などの惑星の影響は考えない。彗星と流星物質との間の万有引力や反作用も無視できるとする。彗星の軌道は不変とする。

 

　さて、前回の最後に、ケプラーの第３法則が成立していることの検証をするため、周期Pを導出した。以下、式の番号が(7)以 下のものは前回と共通である。

 

これに、Qの表式、

 

 

を代入すると、Pをｖの 関数として表すことができる。その結果は、

 

 

 

となる。この式は、人工惑星の場合に近日点（太陽からqの 位置にある）での速度vを選ぶことにより（方向は、太陽の方向に直角とする）、その周期P を制御できることを意味する。 ここで、v₀は、前回と同様、軌道が半径ｑの円軌道の天体（今回は惑星）の速度で、前回述べたように、

 

 

の関係がある。GMは、万有引力定 数と太陽質量との積である。ｑとv₀は あらかじめ与えられた定数として考えるので、(7’)式で独立変数はｖだ けである。

 

６．流星物質放出の「アッシャー理論」近似

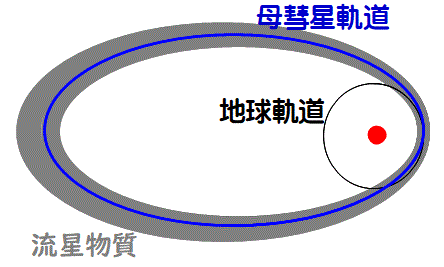
　ペルセウス座流星群は、母彗星である109P/スウィフト・タットル彗星が出すチリがその起源とされている。ところが、母彗星は、周期が約133年 で、この周期で地球に近づくだけである。しかし、ペルセウス座流星群は毎年地球で出現する。これはなぜであろうか。それの考えられる説明は、「母彗星から出た流星物質が軌道全体に振りまかれている」ということだろう。しかし、そんなことが起こるのだろうか。母彗星から出たチリが同じ軌道上の彗星の反対側にまで達するというのは、なにか不自然な説明のように感じられる。

替わりに 次のように考えてはどうだろう。近日点付近で、太陽にあぶられて彗星から流星物質が飛び出すのであるが、その際に、流星物質は彗星に対していくらかの相対速度を持って飛び出すので、流星物質のvは、 彗星の速度vの周りに多少広がった領域の値となる。この領域 を、v-Δv〜v+Δv　と表現しよう。Δvが近日点通過時での彗星からの流星物質の放出速度であって、その方向が母彗星の近日点での進行方向と同じ（あるいは逆向き）になっているとこうなる。それは、図らずも、アッシャー理論と同じ１次元近似になっている。アッシャー理論はホーマン軌道理論であると言ってもいいくらいだ。

このｖの 広がりに対応して、式(7’)に従って、周期PもP-ΔP〜P+ΔPの 広がりを持つはずである。周期に幅があるというということは、流星物質は、次回の回帰で、母彗星より少し早く帰ってきたり少し遅く帰ってきたりするいろいろな成分があって、そして、それが長い年月を経て何回も回っているうちに、早いほうはどんどん早く帰り、遅いのはどんどん帰りが遅くなり、そのうちに、長距離のトラックレースでトップが周回遅れに追いつくようになって、毎年、流星物質のなにがしかの部分が、地球が彗星軌道の近くを通った時に観測されるのではないだろうか。トラックレースではまさに全周に選手が振りまかれたような状態になる。ペルセウス座流星群の場合、母彗星の近日点は、地球軌道の近くにある。ホーマン軌道の性質では、近日点で速度Δvを進行方向に平行に変えても近日点の位置は不変であるので、地球軌道で 流星群の観測される可能性についてはΔvの影響をほとんど受けない。ただ、周回時間Pだけが変化し、そして、1周期の後に、流星物質はΔＰずれたタイミングで同じところに帰ってくる。近日点から離れているところでは、Pと同時にQも変わるため、流星物質は空間的に広がる。そのイメージを図３に示す。

 

７．微分による周期の広がりの計算

　ｖがv-Δv〜v+Δvに 変化する時に、PがP-ΔP〜P+ΔPに 変化するとして、このΔｖとΔPの関係を得るた めには、適当に具体的な数値を代入して計算するのも一つの方法であるが、微分の知識を使うともう少しスマートに計算ができる。但し、Δv、ΔPは、 それぞれ、v、Pに 比べて十分小さな量だとする。微分の知識によると、

 

 

である。これは、近似的関係だが、便宜上、 イコール記号を使う（正しくは、≓だと思ってほしい）。結局、(7’)式をvで 微分すればよいことになる。ただ、このままでは、Pやｖの 数値を考える時に単位とかが面倒になるので、上の式を少しだけ変形して、

 

 

としておく。もちろん、(8)と(8’)は同等だが、こうしておいたほうが、あとの計算がずっと楽になる。

　さて、あとは、(7’)のvでの微分を決行すればよい。分母は、括弧内の 量の3/2乗になっていて、分子は定数なので、見た目より計算は楽である。マ イナス3/2乗の微分は、-3/2が前に出て後はマイナス5/2乗である。根号内の微分を掛けることだけは忘れてはいけない。

 

 

となる。次にPで割り算するので、先に係数の約分とかはしないほうがよい。これに、(8’)式の中のv/Pを掛けると、

 

と驚くほど簡単になる。ここでは、根号の計 算はせずに済むし、Pで割ったおかげで、根号自体が消えてしまった。よって、我々が求める式は、

 

 

となる。また、この式を見ていただけるとわかるように、周期と速度がΔ付きのものと本 体との比率で表されている ので、Pとｖの単位に何を使ってもよいのである。また、それらの間の係数も、速度の２乗だけを含む比率なので、単位に依らないことは明瞭である。

 

８．ペルセウス座流星群への応用計算

　さて、あとは、(9)式の右 辺に数値を代入するだけである。ｖは、母彗星スウィフト・タットルの近日点での 速度、Δvは彗星から放出される流星物質の彗星に対する 相対速度である。v₀は、 ケプラーの第３法則を使って円周を周期で 割り算することで計算できる。楕円軌道においては、vはその√(1+e)倍、すなわち、

 

 

となる。ここで、eは楕円軌道の離心率である。なお、この式は、qが同じでｅが異なる軌道の間で成り立つ。これは、前回の(7)式の導出でvが左辺に来るように変形し、ケプラーの第3法則をPに 適用して、

 

 

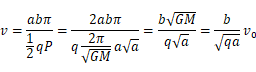
と変形したのち、

 

 

を代入すれば得られる。a=q(1-e)　が離心率ｅの 定義だと思ってよい。

スウィフト・タットル彗星の1998年の軌道データによると、q=0.958天文単位。これに対応する円軌道の周期は、0.938年だから、v₀=30.4km/s、離心率がe＝0.964だ から、v=42.6km/sと なる。ここでv₀が地球の公転速度29.8km/sに極めて近いことを確認しておく。ただし、彗星の軌道の方向は地球軌道付近で平行に接しているわけではなく、進行方向はまったく違う。

　Δvは今までの流星群の出現の経験則から、流星物質の主要部分の彗星に対する相対速度はΔv=20m/s程度（あるいはそれ以下）であるらしい （ここで単位は、km/sではなく、m/sな ので注意）。また、分子運動の熱力学から、60m/sを越える流星物質は放 出されることはないと理論的に予想されている。だから、ここでは、Δvは典型的に20m/sで、最大でもその３倍程度にまでしか分布していないと考えよう。この値でΔv/v＝0.000469となる。１よりかなり小さな値であることを確認しておく。そうでないと、上の１階微分の近似が成り立たない。

　(9)式 の右辺の中央の分数式は、彗星ごとに定数になり、スウィフト・タットル彗星では、これは、164で ある。これが、Δv/vのΔP/Pへの拡大倍率となる。これが１より相当大きな数であることが、流星物質の広がりを示すカギとなる。ΔP/P＝0.0768と なる。これでも１よりはかなり小さいと言える。

　トラックレースで遅れた者が早い者に追いつかれる「周回遅れ」が発生するのは、ΔP/Pが周回の積算（ｎ周回るとnΔP/P）で0.5（半周遅れと半周進み）に達する時である。だから、0.5をΔP/Pで割り算して、スウィフト・タットル彗星が約6.5周すると、計算上は周回遅れが発生し、図３のように流星物質は全軌道上に広がり、ペルセウス座流星群は母彗星がどこにあっても毎年出現するようになる。それに要する時間は、周期の6.5倍、つまり約879年で ある。

　おそらく、ペルセウス座流星群は、これよりもずっと長い出現の歴史を持っていて、だいたいこのような原理によって、現在、毎年我々の目を楽しませてくれているのであろう。以上の数値を他の流星群とともに表にまとめ た。

表：流星群のパラメータの表。各行は、上から、ペルセウス 群、しし群、ジャコビニ（10月りゅう）群、ふたご群。各列は、左から、流星群略称、母彗星、同軌道元期、近日点距離、離心率、対応円軌 道速度v₀、近日点速度、拡大率（本文参照）、近日点速度のバラつき、周期のバラつき、必要周回数n， 周期、周期のn倍。ファエトンは、普通は小惑星として分類されているが、彗星活動によるとみられる増光が観測されている。