太陽系天体の軌道6要素について
上原 貞治
太陽系にあって太陽の周りを回っている惑星、彗星、小惑星などの天体を軌道の特徴を簡単に表すパラメータとして、軌道6要素というものがある。これがなぜ便利かというと、この6つの数値があると、これらの天体が近い将来と近い過去において、どういう空間位置を通っていくのかを、万有引力の法則に従って2体問題の範囲では完全に計算できるからである。また、地球は既知の軌道を進むので、地球から見た惑星、彗星、小惑星などの天体の位置、つまり、どちらの方向にこれらの天体が見えるかということも計算できる。しかも、例えば、今晩、あるいは30日後の夜に望遠鏡で観測する場合に、実用上問題のない精度で予報が出せる。また、地球の軌道も近似的には軌道6要素で表現できる。
もう一つの利点は、軌道6要素は、空間的作図が容易で、彗星や小惑星などの場合、慣れると数値を眺めるだけで、天体の運動や、地球との位置関係の概略が、フリーハンドの作図でイメージがつかめるくらいになる。昨今は、軌道計算は、すべてコンピュータの計算結果がウェブで得られるので、自分で計算する必要はないのであるが、その複雑に見える結果もただ6つの数値からから計算可能で、その概略は多少の心得があれば人間の勘で理解できるものであることを知っておいても無駄ではないだろう。
実際には、6要素の根拠になる天体の2体問題というのは近似であって、3つ以上の天体の重力の影響で、天体の軌道運動はもっともっと複雑になる。しかし、それは、この軌道6要素が時間とともに変動すると考え、一定の期間ごと(たとえば1カ月ごと)に6要素を改訂することにすれば、その複雑な効果を取り込むことが出来る。さらに、この6要素の変化の傾向を見ることも一つの興味深い研究方法である。
前置きが長いのはよろしくないので、本論に進みたい。
1.彗星の軌道6要素
軌道6要素というと、彗星の方式がもっとも有名であり、かつ便利なので、これを基本として最初に説明する。彗星に使われる軌道6要素は、ほぼ例外なく次のようになっている。
- 軌道の形 −− 2変数 近日点距離と離心率
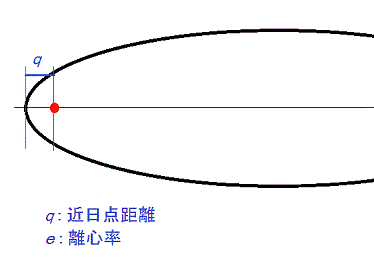
図1: 天体(たとえば彗星)の近日点付近の軌道。赤丸は太陽を表す。
彗星の軌道の形は、円、楕円、放物線、双曲線の4種類がある。彗星の軌道上の位置のうち、太陽にもっとも近い場所における太陽との距離が近日点距離である。伝統と、計算の便宜に従い、km単位ではなく、天文単位(地球太陽間距離の平均距離。1天文単位=149597870.7 km )を使うことになっている。
離心率は、円、楕円、放物線、双曲線の形の区別を表す変数で、通常、eで表し、e=0が円、0<e<1が楕円、e=1が放物線、e>1が双曲線に相当する。彗星等は自然物なので、ちょうど正確にe=0.0の天体やe=1.0の天体が存在するとは考えられないが、かなり、あるいは非常にそれに近い場合があり、その時は、e=0.0 あるいは、e=1.0 として、計算する場合が実際にあり、その時は、計算上は、完全な円あるいは完全な放物線としての扱いになり、特別な注意が払われる。
- 軌道面とその向き −− 3変数 昇交点黄経、軌道傾斜、近日点引数
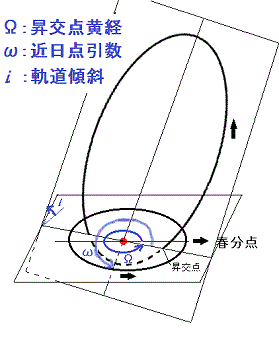
図2: 水平面っぽいのが地球の公転軌道面。立っているのが天体(たとえば彗星)の軌道面。赤丸は太陽を表す。
彗星も惑星も、太陽を含む平面内で運動する。実はその動きは2次元である。しかし、この2次元平面は3次元空間に収まっており、かつ、どっちの方向を向いている場合もありうる。その方向をこれら3変数で指定する。地球の軌道が収まっている平面を基準面(水平面)と考え、天の北極側、つまり、地球であると北極や日本があるほうが上、星座でいうと、北極星や北斗七星があるほうを上にとる。この時、彗星が地球の軌道面を下から上に通る点が昇交点である。昇交点の方向を経度として考え、春分点の方向を0度として地球の公転方向に沿って昇交点まで測った角度が昇交点黄経である。地球の公転方向は上から(北から)見ると反時計回りである。また、春分点では、春分の時(3月21日ごろ)に、地球から太陽を見た方向である。地球から見た方向なので、太陽から見ると逆になり、地球が春分点の方向に来るのは秋分なので間違いないようにしていただきたい。
軌道傾斜は、地球軌道平面と彗星軌道平面の間の角度、つまり、彗星軌道斜面の傾きで表現できる。斜面の傾きは、斜面に対する垂線が鉛直線に対してどれだけ傾いているかの角度で表現する。通常は、傾きは0°〜90°までの範囲となるが、軌道要素の場合は、0°〜180°の範囲にとり、彗星の回る方向まで考えに入れることになっている。たとえば、地球と同じ平面を運動しているが、太陽に近いところで、地球と逆向きに回る彗星の軌道傾斜は180°、つまり、軌道面がまるまる裏返っていると見るのである。軌道傾斜が90°の時は彗星は垂直に立った軌道面を動くので、地球に比べて同じ向きに回っているか逆向きに回っているのか言うことはできない。
最後の近日点引数というのも角度である。ここでいう引数は、ある基準点から現在位置までの間の角度のことで、昇交点から上に上がってきた彗星が近日点をに達するまでに、太陽の周りを実際の角度でどれだけ回ることになるかという角度である。0°〜360°のあいだの角度になる。実際には、昇交点を通る以前に、近日点を通っている場合が半分くらいあるので、その場合は、近日点引数は負の数の角度になるが、360°を足して、正の数にする。−14°なら346°と表現する。負の角度を180°より大きい数値で表現するのは、平面幾何でよく行われることである。
- ある指定時刻の天体位置 −− 近日点通過
以上の5要素で、彗星の軌道と運動は完全に決まるが、他の天体との関係や人間による観測を考えると、もう1つ変数が必要である。それは、ある時点で、天体が軌道上のどこにいるかということである。彗星の場合は、近日点通過(日時)という時刻でそれを指定する。つまり、「この近日点通過の日時に、ちょうど近日点にある」ということを主張するのである。近日点通過は、普通に、西暦何年何月何日何時何分何秒ということでよいが、便宜上、天文学では、地球時あるいは力学時と呼ばれる、世界時からうるう秒の効果を除いた時刻表示(理想的には地球近傍で重力の影響の小さい宇宙空間に置かれた原子時計に同等)に従う。なお、空間を光が伝わるには時間がかかるので、そのぶんは常に補正して、実体の場所を考えるものとする。
彗星については、以上で6要素になる。実は、完全に円軌道の彗星の場合は、近日点がどことも言えないので、近日点引数と、近日点通過が指定できなくなる。その場合の解決法は、下の3節に書く。なお、近日点距離については、円の半径を採用して何の支障もない。
2.小惑星あるいは惑星の6要素
小惑星というのは、楕円軌道の彗星と軌道の点からすると同じであるので、e<1の彗星に完全に倣ってよいのであるが、小惑星に限ればそれよりも便利な場合が多い表現法があるので、それを紹介する。彗星と違う表現方法も覚えるのが便利なのか、それとも彗星と同じ方式だけにするのが便利なのか微妙なところであるが、実際に違う表現方法が行われているので、こちらも紹介せざるを得ない。
- 軌道の形 −− 2変数 軌道半長径(平均軌道半径)と離心率
楕円軌道の場合は、近日点距離の代わりに軌道半長径が用いられることが多い。 軌道半長径は、軌道長半径と呼ばれることもあれば平均軌道半径と呼ばれることもあり、どれも間違ってはいない。つまり、近日点距離と遠日点距離の平均である。軌道半長径をa、離心率を e とすると、近日点距離は、q=a(1-e)、遠日点距離はQ=a(1+e)で、両者の平均は、(q+Q)/2=aである。離心率とセットで表現すれば、(q, e)の組み合わせでも(a, e)でも簡単に換算できる。なお、彗星の場合は、eが1以上の時に、Qとa がいわば無限大になって数値で表現できなくなるので、彗星にはこの表現は使わないのである。
- 軌道面とその向き −− 3変数 昇交点黄経、軌道傾斜、近日点黄経
小惑星の場合、(惑星でも彗星でもかまわないが)軌道傾斜が0°にたいへん近い場合がありうる。(180°にたいへん近い場合でも同様の問題が起こるが、実際にはこれは極めてまれである) この場合は、昇交点の定義が困難になる。しかし、正確に0°あるいは180°でない軌道傾斜を与える場合は、どうであれ、昇交点の方向を与えないと意味がないので、不正確であっても昇交点黄経を与える。この昇交点黄経が少々間違っていても、軌道傾斜が小さければ、実害はあまりないという事情がある。 その場合、昇交点の位置がわからないと近日点引数もはっきりしないことになる。しかし、実際には、楕円軌道の小惑星の場合、昇交点があやふやでも、近日点の位置ははっきりわかる場合が多い。そういう時は、近日点引数ではなく、近日点黄経を用いる。近日点黄経の定義は、昇交点黄経を与えた時は、昇交点黄経+近日点引数のことである。軌道傾斜を与え、昇交点黄経を与えた場合は、近日点引数を与えても近日点黄経を与えても、数学的には同等であるが、前者を与えると、昇交点黄経と近日点引数という精度の悪い数値を2つ与えることになるのに対し、後者を与えると、近日点黄経は正確に決まるので、あやふやな変数が昇交点黄経1つで済むという利点がある。
また、軌道傾斜が0°にたいへん近いということしかわからず、約0°ということにしてしまったとすると、昇交点がまったく定義できなくなる。この場合は、昇交点黄経は与えず、近日点黄経のみを与える。軌道傾斜が本当に0°だとすると、任意の方向を昇交点と考えてよくなり、昇交点は決まらないけど、近日点黄経は実際の近日点の黄経として決定され、しかも、任意の(いい加減に与えた)昇交点黄経値を用いても常に、 近日点黄経=昇交点黄経+近日点引数 の関係が成り立つ。(なお、足し算の結果が360°を超えると、そこから360°を引いて表現する)
- ある指定時刻の天体位置 −− 平均近点角
彗星はだいたい近日点の近くで注目されるので、近日点通過時刻が重要な変数であるが、小惑星の場合は、必ずしもそうでないので、近日点とはまるっきり違う方向でも表現できるように、平均近点角を使う場合が多い。平均近点離角とも呼ぶ。これは、ある適当に便利なように与えた元期(=観測時に近いある定義された基準時刻)の天体の位置を近日点から測った角度で表現するものである。しかし、平均近点角は、分度器で測るような本当の角度ではなく、仮想的な角度であって、時間とともに一定の速度(つまり平均速度)で進む角度である。1公転周期を360°として、それを時間で均等割にしたものなので、実は角度ではなく、近日点からの経過時間を周期で割ったものをそれに360°をかけて角度で表現したものと言ったほうがわかりやすいであろう。
たとえば、マラソンのコースがあるとする。コース全長は42.195kmである。ある選手があるレースで、このコースを2時間12分00秒で走ったとする。その選手は、実際には加速したり、スピードを緩めたりしながら走ったであろうが、同じ記録時間で、等速で走る分身選手を想定し、同時刻におけるその分身の位置を本人の位置の代わりに用いるのである。実際には、本人と分身が同じ場所に重なるのは、スタートとゴールだけかもしれないし、途中でも抜きつ抜かれつするかもしれないが、たとえば、この分身のスタート後1時間06分00秒後の平均近点角は必ず180°である。ただし、スタート地点を近日点に対応させる。平均近点角というモノサシは、マラソンコースを1周42.195kmの円形のコースとし、そこを選手が自分の最終記録で等速円運動した場合の角度と見れば良い。
なんでそんなことをするかというと、分身選手の位置は時間で簡単に計算でき、かつ、天体の場合は、分身位置から本人位置を求める計算も比較的簡単であるからである。分身は平均角速度で走るので「平均近点角」である。本人のいる実際の角度は「真近点角」と呼ぶ。(この両者の換算法は、たとえば、Wikipediaの「離心近点角」を参照)
以上、いずれにしても合計6変数である。 なお、ここで述べた周期は、軌道半長径からケプラーの第3法則を使って求める。周期は重要な軌道パラメータであるが、通常、軌道6要素には含めない。
3.円軌道の場合
軌道の形が完全な円形である時を考える。
- 軌道の形 −− 実質1変数 軌道半長径(平均軌道半径)、離心率はe=0
軌道半長径は、単に軌道半径のことである。円軌道と言えば離心率は0に決まっているので、数に入れない。
- 軌道面とその向き −− 2変数 昇交点黄経、軌道傾斜
近日点の向きが決まらないが、決まらないものを決める必要はなく、それは省略してよい。
- ある指定時刻の天体位置 −− 平均黄経
近日点が決まらないので、平均近点角は使えないので、代わりの角度、通常は、元期(基準時刻)の天体の位置を黄経で表現する。平均黄経というのは、地球の軌道面と春分点の方向を基準にした座標系(昇交点黄経の定義に用いた基準と同じ)での経度である。昇交点の場合は、黄緯はかならず0であるが、この場合は、一般的にはそうではない。平均黄経の「平均」は、平均近点角とは意味が違って、地球軌道面の座標系を示す言葉であるが、正確な定義が必要ならそれを確かめるべきである。今回のところは、普通の黄経と考えて支障ない。
円軌道の実際上の計算の場合は、どこを近日点と考えてもよいので、元期の時点を近日点と考えて、元期を近日点通過と見なし、天体軌道面上での昇交点からそこまでの角度を求めて近日点引数とすると、円軌道の小惑星も楕円軌道の彗星のように計算できることは明白であろう。
従って、円軌道の場合は、実質4変数である。
4.力学的おまけ
最後に、なぜ軌道要素が6つなのか物理学(ニュートン力学)の観点で考えてみよう。太陽系の天体の軌道は、ある時点(元期)でのその天体の空間位置座標と速度ベクトルが決まるとその前後の運動は完全に決まる。空間座標も速度ベクトルも3次元座標なので、変数の自由度は3+3=6である。従って、これによって決まる軌道要素の自由度も6になる。
円軌道の場合は、空間位置はどこでもよいが、円軌道になるような速度は、太陽の方向に対して直角方向の決まった速さのベクトルに限られる、つまり、方位角という1つの自由度しか持たない。したがって、円軌道の自由度は4であり、軌道要素の自由度も4である。
いっぽう、軌道傾斜0°というのは、そういう物理的な根拠のあるものではなく、たまたま地球の軌道平面に一致したという見かけ上の都合によるもので、これによって、昇交点黄経は決まらなくなり指定の必要もなくなるが、それは座標系による見かけの特異性と言われるもので、天体そのものの物理的な実態のある現象は伴わない。
(終わり)
今号表紙に戻る

