原著　J. Keill, 　蘭語訳　J.Lulofs

翻案著者　 志筑忠雄、現代語訳・監修　上原貞治

　

　

　第２回（前号）では、幾何学上の楕円の性質について検討したが、今回も第６節でそれを続ける。そして、第７、９節で、それは力学と融 合して議論され、ケプラーの第１法則（楕円軌道）から、ニュートンの万有引力の逆２乗則が導かれる。

　なお、「暦象新書」では、下編上巻で「半正方」(＝c)を定義しながらも、下編下巻の計算式中ではおもにその２倍の長 さ（＝「正方」）を用いているので、以下の現代語訳でも、原文に忠実に数式中で(2c )を約分せずに残してい る。計算の理解のためには、もちろん適宜約分していただいて問題ない。

　

６．第五の定理：楕円の半正方　（全４段）（下編上巻「求心常経張本」より）

・[図5-19]

　

　

　

　

　

　

　

　

　

　



［図5-19］第三紙（六）

　

　

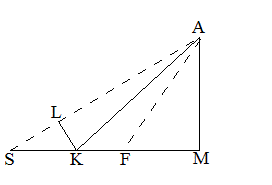
ALは常に半正方に等しい。AL＝c 。　（c は半正方。以下においても同じ）

　図の解説は第４段にある。

　

　第１段：中離時の半正方

・［図5-16］

　

　

　

　

　

　

　

　

［図5-16］第三紙（三）

　

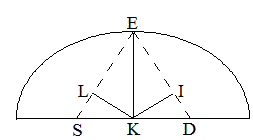
　物体が楕円の正脇点（点E）にある時を「中離時」という。（「中離」は「平均距離」と同じ意味）点Sと点Dは焦点である。

　KI⊥ED、KL⊥ESである。Kは楕円の中心である。ここで「第四の定理」の第３段によると、ED＝ES＝a。だか ら、ES：EK＝EK：ELより、a：b＝b：EL

ゆえに、　EL＝b²/a， 　（EIも同じ）　EL、またはEIの長さを「半正方」と呼ぶ。（以下、c とする）よって、

　a：b＝b：c

　物体が正脇点になくても、［図5-19]のALのような長さは常に半正方である。このことは以下に詳しく述べる。

　

　第２段：大小の直角三角形の比例（一）

・［図5-17］

　

　

　

　

　

　

　

　

　

　

　

［図5-17］第三紙（四）

　

　AI：AM＝e：a

　

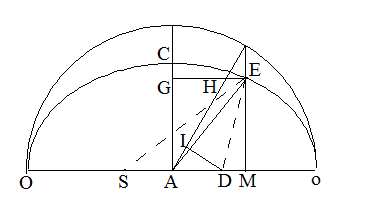
　DI⊥AH、EM⊥Oｏ。Aは楕円の中心である。ここで、「第四の定理」の第４段によると、

　　 GH：GE＝b：a　　･･･　�@

また、同定理の第２段によると、AH＝ACである、ゆえに、直角三角形　△AGE、△AGHを考えると、

　GE²−GH²＝AE²−AC²，　（AC²＝AH²　だから） 　

そして、同定理の第４段の結論によると、EA²−CA²＝AI² 。ゆえに、

　GE²−GH²＝AI²　　　･･･　 (甲)　　また同定理の第３段によると、

　a²−b²＝e² 　　･･･(乙)

�@によって、(甲)、(乙)を考えると、

　AI：GE＝e：a

GE＝AMであるから、AI：AM＝e：a　がわかる。

　

　第３段：大小の直角三角形の比例（二）

・［図5-18］

　

　

　

　

　

　

　

　

［図5-18］第三紙（五）

　

　

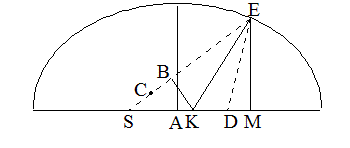
　AM：BC＝a：e

　

　EKは点Eの垂線である。（点Eにおける接線の垂線を略してこのようにいう）　点Sと点Dは焦点である。KB⊥ES。SCは中離時の SL［図5-16］に等しい。ここにおいて、「第四の定理」の第９段によると、ES：SK＝ED：DK。ゆえに、

　ES＋ED：ES＝SD：SK，（第６段によると、ES＋ED＝2a、SD＝2e）ゆえに、

　a：ES＝e：SK，　（e＝SA　だから）　ゆえに、

　ES：SK＝a：e　･･･　�@

　△KBSと△EMSは、相似の直角三角形だから、

�@と合わせて、 ES：SK＝EM：KB＝SM：SB＝a：e

　物体Eがどこにいてもこの関係が成り立つから、中離時において同等の比例式を考えると、それは E'S：SA＝E'A：AL＝SA：SL＝a：e，（E'　は正脇点。点Lについては［図5-16］を参照）だ から、辺々の差を取ると、

　ES−E'S：SK−SA＝EM−E'A：KB−AL＝SM−SA：SB−SL＝a：e　

　SM−SA＝AM，　SL＝SCだから、SB−SL＝BC。これで、

　AM：BC＝a：e　がわかる。

　

　第４段：半正方

・［図5-17, 18］

　BE＝c 　　　（［図5-18］のBE＝［図5-19］のAL＝c ）

　

　まず前段によって、AM：BC＝a：e。また、第２段により、

　AM：AI＝a：e。　ゆえに、

　BC＝AI

　「第四の定理」の第６段によると、AI＋a＝SE。　ゆえに、

　SE−BC＝SC＋EB＝a，　（BC＝AI　だから）　ゆえに、

　SC＋EB＝a

　SCは［図5-16］のSLであるから、これをaから差し引くと、EBは［図5-16］のELに等しい。EL＝c だ から、

　EB＝c

・[図5-19]　

　上のEBはこの図ではALである。よって、AL＝c 。物体が動くと、いろいろな線分の長さは変わるが、この長さは一定であ る。これを半正方という。

　

７．求心力の一般則（下編下巻「求心常経」より）

　すべて求心力によって曲線の軌道（曲線は、円や楕円に限らず、直線以外の線の総称である）を運行する物体にかかる求心力は、その軌道の各点 において、次の２つを合成したものに比例する。(1)物体から中心までの距離に比例、(2)中心から物体のある点での接線に下ろした垂線の長 さの３乗と物体のある点での接円の半径（または直径）の積に反比例。（合成は乗算、中心は求心力の中心である）｛求心力〜SA/(SP³・AR) 　［図6-1］｝

　

・［図6-1］による説明

　

　

　

　

　

　

　

　

　

　

　

　

　

　

　

　

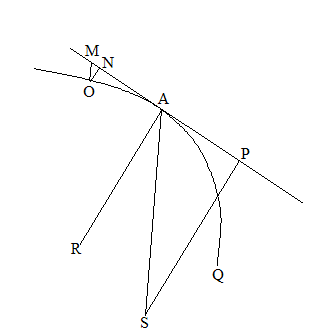
[図6-1]本文総図（一）　｛本連載第４節に出た図4-7に同じ｝

　

QAOは曲線であり、物体が点Sの方向への求心力によって運行する軌道である。Aは、現在、物体がある点である。PMはそこにおける接 線である。AOは、ほとんど無限小の時間に運行する曲線の弧である。ARは、弧AOの接円の半径である。つまり、この弧は、接円の無限小の弧 でもあり、ARはこの弧AOに対応するものである。

　SPは、中心Sから引いた接線への垂線である。また、OM//SA、ON//SP。このとき、OMを点Aにある物体がSに引かれる求 心力であるとする。また、物体が接線をその直角方向に遠ざかろうとする力をON（つまり接円の部分の力）とする。この力はRのほうを向いてい る。Rは接円の中心である。もし、物体がこのままの速さでこの力によって運行するならば、この接円の円周を運行するであろう。この力とSに向 かう力（求心力）との比は、ON：OMである。また、相似関係にある直角三角形を考えると、これはSP：SAに等しい。

　さて、ニュートンの「起源」｛「プリンキピア」｝の第４条によると、円軌道の運動の求心力は (速さ)²/半径　 に比例する。（このために「円運動の求心力」の定理を論じた）そして、速さはSPに反比例する。つまり、1/SPに比例する。（このために 「速さに比例する量」の定理を論じた）　ゆえに、速さの２乗は1/SP² に比例する。ゆえに、ONは、

1/(SP²・ AR)に比例する。

　さて、前に述べたように、SP：SA＝近心力：求心力であり、近心力は1/(SP²・AR) に比例する。また、SP：SA＝1/(SP²・ AR)：SA/(SP³・ AR)である。ゆえに、S方向の求心力は、SA/(SP³・AR)に比例する。

◇円でない曲線は、多くの半径の違う微小な円弧が連続しているものなので、曲線上のそれぞれの点においてそれぞれの接円がある。接円 は、該当する点付近の無限小の弧の両端２点でのそれぞれの接線に垂直な２線を引き、その２線の交点をその中心とするものである。正しい円弧で はないので、この２線の長さも違いがあってよいのであるが、無限小弧に関するものなので、その差も元の半径に比べると無限小に過ぎない。◆

　

　

８．接円半径（下編下巻「相応輪径」より）

・[図6-3]による説明

　

　

　

　

　

　

　

　

　

　

　

　

　

　

　

　

　

　

　

　

　

　

　

　

　

　

　

　

　

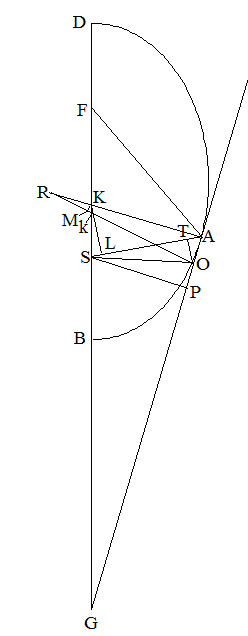
　[図6-3]本文総図（三）

　

　

　DABは楕円の半分である。DBが長径で、点Fと点Sが焦点である。ARとORの２直線はきわめて接近していて、どちらもAGに垂直 である。｛A、Oは、ともに楕円軌道上にあって近接した点である。この時、ARは接円の半径である。接円については、本連載第１回の第４節を 参照｝　また、KL⊥AS、OT⊥AS、KM⊥ORである。ここで、ユークリッド第６巻の第３段によると、SA：SK＝FA＋SA：FS。 （このために「焦点間距離配分の比例関係」の定理を論じた）だから、SA：SKは常に一定の比（楕円周上のどこにおいても変わらないこと）な ので、Aが楕円周上を動く時、SAとSKのそれぞれの長さの変化分同士も同じ比になり、AT：Kｋ＝SA：SK。また、ミルネの楕円解第６巻 の第６段によると、AL＝c 。（このために「半正方」の定理を論じた）　また、KA//SPなので、 ∠ASP＝∠KAL＝∠TOA。なぜならば、∠TAOが∠ASPと∠TOAの双方にとって余角となるからである（余角とは90°との差のことである）ゆえに、KA：AL＝SA：SP。それで、SP＝2c ・ SA/(２KA)。　そして、KA＝2c ・SA/(２SP)である。

　さて、直角三角形の相似関係　△KMｋ∽△GPS　と　△OTA∽△SPAが成り立つ。よって、 KM：Kｋ＝GP：GS＝AP：SK。また、Kｋ：AT＝SK：SA。（前に出た）

AT：AO＝AP：SA。ゆえに、KM：AO＝AP²：SA²。 また、この比は、

＝SA²−SP²：SA²＝SA²−(2c )²・SA²/(４AK²)：SA²。（SP は前に出た） だからこの比は、＝４AK²−(2c )²：４AK²。 （AK：c ＝SA：SP　だから）ゆえに、

(2c )²：４AK²＝AO−KM：AO＝AK：AR。 　よって、AR＝４AK³/(2c )²。

◇ある人が問うに、上で、SAの変化分をATとするのは、SO＝STとしてのことであろう。しかし、OT⊥ASだから、SO≠STでは ないのか。答えて言うに、SOに比べるとOTもATもごく小さいので、長さの差はあるが、その差をATと比べるとまだそれよりもごく小さい。 ゆえに、ATを変化分の長さとする。また、AOは接線であるが、円弧と接線の区別がないのも、またごく小さい区間だからである。ごく小さい、 というのは、無限小ということである。しかし、無限小の次数が同じものは、それらの間に有限の比がある。ATとAO、AOとMKのようなもの がそれである。◆

　

・[図6-4]の説明

　

　

　

　

　

　

　

　

　

　

　

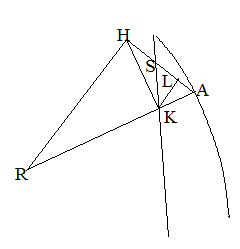
　[図6-4]本文総図（四）

　

　ここにおいて、楕円周の各点における接円の半径を求める作図法を得た。AKは物体のある点での接線の垂線で、長径の軸と点Kで交わ り、HK⊥AKで、HはASを延長した直線上にある。RH⊥AHとする時、ARがその半径である。（このために「接円の半径」の定理を論じ た）

　

９．本来の例：中心が楕円焦点の場合〔ケプラー運動。ケプラーの第１法則からの重力逆二乗則の導出〕 （下編下巻「正例心楕臍」より）

・［図6-3］の説明

　物体が一つの楕円形の軌道上を運行し、その求心力が焦点の１つの方向に働いている場合は、その力は中心までの距離の２乗に反比例している。

　その理由は、AR＝2c ・SA³/(２SP³) の関係になっているからである。（この関係の導出についてはあとで説明する）　そうすると、求心力〜SA/(SP³・ AR)＝

SA・２SP³/(SP³・2c ・SA³)であ る。（割り算の商でまた割るので、分母分子が入れ替わる）これはまた、＝２/(2c ・SA²)であ る。（SP³と SAが約分されるから） ここで、２/(2c )は一定なので、これを省くと、求心力〜１/SA² となる。〔ケプラーの第１法則からのニュートンの万有引力の法則の導出〕

◇ AR＝４AK³/(2c )² というのは前に出た。また、AK＝2c ・SA/(２SP)、これも前に出た。ゆえに、AK³＝(2c )³SA³/(８SP³)。 ４AK³＝４(2c )³SA³/(８SP³)。

この両辺を(2c )² で割るとARが得られる。AR＝ ４(2c )³SA³/(８SP³・(2c )²)。　

(2c)² と４が約分されて省かれ、＝2c・SA³/(２SP³)　となる。◆

　

　

　以上、３回の連載を通じて、中心力運動におけるケプラーの第２法則の証明（第１節）とケプラーの第１法則からのニュートンの万有引力 の法則の導出（第２〜９節）を行った。なお、逆は必ずしも真ならずで、ニュートンの万有引力の法則の下では、放物線軌道と双曲線軌道も許され るので、楕円軌道がユニークに導かれるわけでない。しかし、放物線も双曲線も広い意味では、楕円と同等の２次曲線である。

　

　もともとは、ここで連載を終える予定であったが、ケプラーの第１、２法則だけ学んで、第３法則の証明を学ばないのは、あまり気持ちが すっきりしないので、この目的のために、もう１回だけ連載を延長することとする。

（つづく）

　

付録：原典資料紹介（その３）

　

　

志筑忠雄「暦象新書」下編下巻「相応輪径」より幾何学の比例式の多いページ（『暦象新書』写本、早稲田大学古典籍総合データベースよ り）

　

J. Lulofsオランダ語訳本"Inleidinge tot de waare natuur- en sterrekunde, of de natuur- en sterrekundige lessen”(グーグルブックス）より 上の「暦象新書」(志筑版）の部分に対応する付近。「ジョン・ケイルからエドモンド・ハリー氏への手紙」という章に収められている。