�@
���{�̌ÓT�Ŋw�ԓV���w�i��Q��j
�@
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�����@J. Keill, �@�����@J.Lulofs
�|�Ē��ҁ@
�u�}���Y�A������E�ďC�@�㌴�厡
�@
�@��P��i�O���j�ł́A���S�͂ɂ�镨�̂̉^���̉���Əؖ��Ƃ��āA�P�v���[�̑�Q�@���̏ؖ��ƁA�~�^���̊w���������B�܂��A�u�~�O���Ƒȉ~�O���ɂ���������̈�v�̂��߂̒藝�v�̂��߂́u���̒藝�v���ؖ��������A�u�����̈�v�̏ؖ��v���g�́A�{�e�̓��ʂ̖ڕW����͂͂��ꂽ�e���ɂȂ�̂ŁA���r�ł��邪�ȉ��ȗ��Ƃ������Ƃɂ����Ă��������B
�@����́A���悢��{���ł���P�v���[�̑�P�@���i�f���̑ȉ~�O���j���疜�L���̖͂@���̏ؖ��̂��߁A�ȉ~�̊w�I�����̏ؖ��ɂ�����B
�@
�T�D��l�̒藝�F�ȉ~�̏œ_�ԋ����z���̔��W�i�S�X�i�j�i���ҏ㊪�u���S��o���{�v���j
�E�m�}�n5-15]
�@
�@
�@
�@
�@
�@
�@
�@
�@
�@
�@
�@
�@
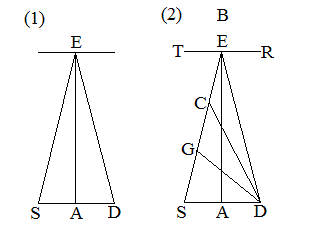
�@�@�m�}5-15�n��O���i��j
�@
�@SA�FSK��FA+SA�FFS
�@�}�̉���͑�X�i�ɂ���B
�@
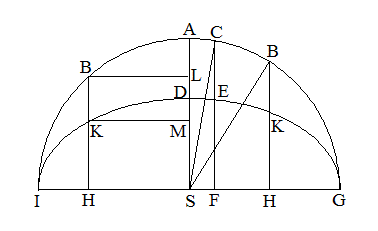
�@��P�i�F�O�ډ~�Ƒȉ~�̔��W
�E[�}5-5]
�@
�@
�@
�@
�@
�@
�@
�@
�@
�@
�@
�@
�@
�@�@�@�@
�@�@�@�m�}5-5�n��i��j
�@
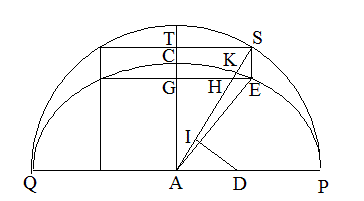
�@S�͑ȉ~�Ƃ��̊O�ډ~�̒��S�ł���BGI�͑ȉ~�̒��a�i����2a�j�ł���A�O�ډ~�̒��a�ł���BDS�͑ȉ~�̔��Z�a��
����B�i�Ȍ�Aa��ȉ~�̔����a�Ƃ��Ab�Z�a�Ƃ���j����ɂ����āAHK�FHB��FE�FFC��
SD�FSA��2b�F2a�B�i�}�̍��E��HKB�̂��ꂼ��ɂ����Đ��藧�j2a�͊O�ډ~�̒��a��
����B�䂦�ɁAMD�FLA��SM�FSL��2b�F2a�B
�@
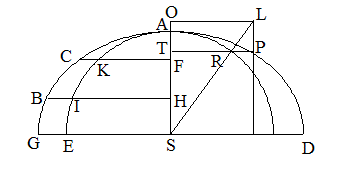
�@��Q�i�F���ډ~�Ƒȉ~�̔��W
�E�m�}5-6�n
�@
�@
�@
�@
�@
�@
�@
�@
�@�@�@�@
�@�@�@�@�m�}5-6�n��i��j
�@
�@
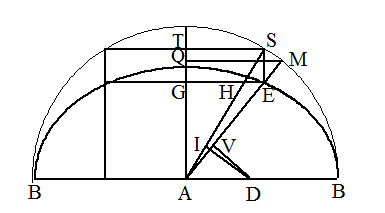
�@GD�͑ȉ~�̒��a�i2a�j�ł���BAS�͑ȉ~�̔��Z�a(b)�ł���A���ډ~�̔��a�ł���B����ɂ���
�āAFK�FFC��HI�FHB��SE�FSG��2b�F2a�B2b�͓��ډ~�̒��a�ł���B
�@�䂦�ɁA�܂��AKC�FIB��FC�FHB��FK�FHI�B
�@�܂��A���Ƃ���SR���������āASL��SD�ƂȂ�_L���߂�ƁART�FLO��RT�FPT��ST�FSO��SR�FSL��(���ډ~��
�a)�FSL��2b�F2a�B
�@
�@��R�i�F�o�S��
�E[�}5-7]
�@
�@
�@
�@
�@
�@
�@
�@
�@
�@�@�@�@
�@�@�@�@�m�}5-7�n��i�O�j
�@
�@
�@R�͑ȉ~�̒��S�ł���BRC��IG�B�܂��ACD��CS��a�Ƃ���ƁA�_S�Ɠ_D�͂Q�̏œ_�ł���B�����ŁARD�@��
�邢��RS�̒������u�o�S���v�ƌĂԁB�i����A�����e�ŕ\���j�����a�A���Z�a�A�o�S���͒��p�O�p�`�̊e�ӂ̊W�ɂ���B�oa2��b2�{e2�@�p
�@
�@��S�i�F���S����̋����̂Q��̍�
�E[�}5-8]
EA2�|CA2��AI2�C(CA��b�j
�@
�@
�@
�@
�@
�@
�@
�@
�@
�@
�@�@�@
�@�@�@�@�m�}5-8�n��i�l�j
�@
�@
�@AS�͊O�ډ~�̔��a�ł���A�ȉ~�̔����a�ɓ������BDI��AS�BD�͏œ_�̈�ł���B��P�i�ɂ���āAAG�FAT��2b�F2a�B
����āAGH�FTS��2b�F2a�BTS��GE�B�䂦�ɁA
�@GH�FGE��2b�F2a�@�@����@�@
�@���p�O�p�`�̕ӂ̊W����A
�@AH2��GA2�{GH2�B�@
��Q�i���A�@AH��AC��b�B�@�䂦�ɁA
�@AC2��GA2�{GH2�B�@����A
�@AE2��GA2�{GE2�@�@
�@AE2�|AC2��GE2�|GH2�@����@�A�@�@
�@�@�@
�@���AGE2�|GH2�FGE2��a2�|b2�Fa2
��R�i�ɂ��Aa2�|b2��e2
�@GE2�|GH2�FGE2��e2�Fa2�@����@�B
�@AS��a�B�@ST��GE�B�@DI��AS�B�@AI�FAD��ST�FAS�B
�@AI2�FGE2��e2�Fa2�@����@�C�C
�@�iGE2��ST2�Ce2��AD2�Ca2��AS2�@������j
�B�A�C���A
�@GE2�|GH2��AI2
�A���A AE2�|AC2��GE2�|GH2
����āA EA2�|CA2��AI2 �@
�Ƃ������Ƃ��킩��B�i�_E���ǂ��ɂ����Ă����ꂪ���藧�j
�@
�@��T�i�F���ϋ����Ƃ̔��W
�E[�}5-9]
�@AI�FAV��AE�Fa�C�@�iBA���u���ϋ����v�Ƃ����B����͔����aa�ɓ������j
�@
�@
�@
�@
�@
�@
�@
�@
�@
�@
�@�@�@
�@�@�@�@�@�m�}5-9�n��i�܁j
�@
�@
�@VD��AE�B�@QM��TA�B�����ɂ����āA�Q�̒��p�O�p�`�@��AVD�Ɓ�AID�́A�Εӂ����L���Ă���B�܂��A
��AVD�䁢QMA�B��AID �䁢STA�B�iAS��AM�j
�䂦�ɁAAI�FAV��ST�FMQ�@�ł���BST��EG������A
�@AI�FAV��EG�FMQ�@����@�@
�܂��AEG�FMQ��AE�FAM�@����@�A�C�@AM��a
�@�A�A���
�@AI�FAV��AE�Fa
�@
�@��U�i�F�œ_����̂Q�����̘a�͈��
�E�m�}5-10�n
�@ED�{FD��2a
�@
�@
�@
�@
�@
�@
�@
�@
�@
�@
�@
�@
�@
�@
�@
�@
�@�@�@�@
�@�@�@�@�m�}5-10�n��i�Z�j
�@
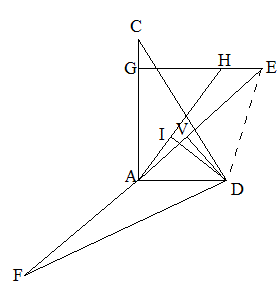
�@����EF�ɂ����āAEA��FA�Ƃ���BE�͕��̂�����_�AD�͏œ_�AA�͑ȉ~�̒��S�ł���BAC��b�Ł@AC��AD�B
�O�����̒藝�ɂ��A
�@CD2��CA2�{AD2
�@ ED2��VD2�{VE2�@����@
(�b)
�@FD2��VD2�{VF2�@����@
(��)
�@VD2��DA2�|AV2�@����@�@
�@VE2��AE2�|(AV2�{�QAV�E
EV)�C�@�i (AV�{EV)2��AE2�@������j
��S�i���A�@AE2��CA2�{AI2
�@VE2��CA2�{AI2�|(AV2�{�QAV�E
EV)�@����@�A
�@�{�A���A
�@ED2��a2�{AI2�|�QAV�EAE
�C�@�iED2��VD2�{VE2���(�b)�Ca2��DA2�{CA2�C
�QAV�EAE���QAV2�{�QAV�E
EV�@������j
�@VD2��DA2�|AV2�@����@�@�@
�@�i�O�ɏo���j
�@VF2��
(VE�{�QAV)2
�@������AVF2��VE2�{�SAV2�{�SAV�EEV
�A�����̉E�ӂɑ������ƁA
�@VF2��CA2�{AI2�{�RAV2�{�QAV�EEV
�@����@��
�@FD2��VD2�{VF2�@����@
(��)
�@�{�����A
�@FD2��a2�{AI2�{�QAV�EAE
�@�@�@�@�ia2��DA2�{AC2�@������j
�܂��A��T�i����A
�@AI�FAV��AE�Fa�B�@������AAV�EAE��AI�Ea
�@ED2��a2�{AI2�|�QAI�Ea
�@FD2��a2�{AI2�{�QAI�Ea
������AED��a�|AI�C�@FD��a�{AI
������AED�{FD��2a
�@
�@��V�i�F�Q�œ_����̒����̘a�͈��
�E[�}5-11]
�@DE�{SE��2a
�@
�@
�@
�@
�@
�@
�@
�@
�@
�@
�@�@�@
�@�@�@�@�@�m�}5-11�n��i���j
�@
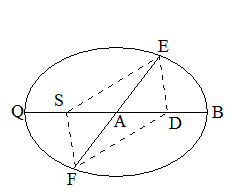
�@�_S�Ɠ_D�͂Q�̏œ_�ł���BSE//DF�ASF//DE�ł���B������ASE��DF�ASF��DE�B�䂦�ɑO�i�ɂ��ƁA�Q�̏�
�_����������ȉ~����̈�_�ւ̒����̒����̘a�́A
�@DE�{SE��2a�C�@DF�{SF��2a
�@�ǂ̓_�ł����̂悤�ɂȂ�B�ȉ~��`�����@�͎��ɏo�Ă���B
�@
�@��W�i�F�ȉ~���̐����̏���
�@�ȉ~����̓_�̐ڐ��ɑ��鐂���́A�Q�œ_����̒����̊Ԃ̊p�������
�@
�@�ȉ~�̕`�@�Ƃ��āA�Q�œ_�ɂP�{���̐j�𗧂āA���a�ɓ����������̎����Q�̐j�ɕt���āA�P�̏����Ŏ�����������A��������
�܁A�Q�̐j�̊O�����͂ނ悤�ɉƁA�ȉ~��`�����Ƃ��ł���B�i��V�i�ɂ��j
�m�}5-12�n�@
�@
�@
�@
�@
�@
�@
�@
�@
�@
�@
�@
�@
�@�@�@
�@�@�@�@�m�}5-12�n
�@
�@�}(1)�̓_E�̂悤�ɁA�Q�̏œ_���瓙�����ɂȂ��Ă���Ƃ��́A�ڐ�//DS�Ȃ̂ŁA����EA����DES���Q��������͖̂��炩
�ł���B
�@���������������͂́A�K���œ_�Ə��������Ԓ�����ɂ�����B�Q�œ_�̂��ꂼ��̔��Ε����Ɉ����͂̍��͂́A�}(2)�œ_B�̕����Ɍ�
�����̂ŁA�����EB�̕����ɂȂ�B�䂦�ɏ������i�ȉ~��`�����Ɂj���������͂���ɐ����ȕ����ŁA�ڐ�RT�̕����ɂȂ�B
�@�����ŁA���Ƃ��P�̏œ_���AG�ɂ����Ă��AC�ɂ����Ă��A���������͂͏��EB�̌����Ȃ̂ŁA����EA�̌����͕ς��Ȃ��B
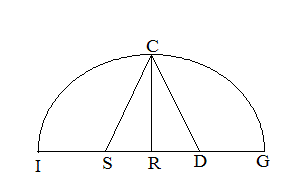
�@���Ƃ��A�~�ɂ����āA
�m�}5-13�n
�@
�@
�@
�@
�@
�@
�@
�@
�@
�@
�@
�@
�@
�@
�@�@�@�@
�@�@�@�@�m�}5-13�n
�@
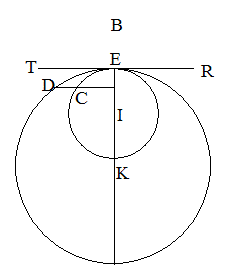
�@�傫���~�̒��SK�ɑ���傫�����a�̉~��ED�ł����Ă��A�������~�̒��SI�ɑ��鏬�������a�̉~��EC�ł����Ă��A�������~�̐�
��RT��ڐ��Ƃ���EK�𐂐��Ƃ��邱�Ƃɂ��Ă͓����ł���B���������A���̒��S�̏ꏊ��m��Ȃ����̂悤�ł���B�傫���~��E�܂ŗ��āA
���邢�͏������~��C�܂ŗ���ƁA���̎��ɏ��߂ĈႢ���킩��B
�@�O�}[�}5-12(2)]�̓_E�̐ڐ����A�œ_�܂ł̋�����m��Ȃ��悤�Ȃ��̂ł���B������A�˂�RT//DS�ł���B�䂦�ɁA
���̏œ_��C�ɂ��낤��G�ɂ��낤���A����ɂ͊ւ�炸�A��ɐ������ȉ~����̓_����Q�œ_�Ɉ������Q�����̊Ԃ̊p���Q�������邱�Ƃ��킩
��B�܂�A���̒ʂ�ł���B
�E�m�}5-14�n
�@
�@
�@
�@
�@
�@
�@
�@
�@
�@�@�@
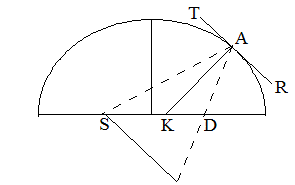
�@�@�@�@�@�m�}5-14�n��O���i��j
�@�@
�@A�͕��̂̂���_�ł���BAD�����������̒�����AS�Ɠ���������ƁA�O�̐}�m�}5-12(2)�n�Ɠ��l�ɂȂ�B������A����AK��
��SAD���Q�������邱�Ƃ��킩�邾�낤�B
�@
�@��X�i�F�œ_�ԋ����z��
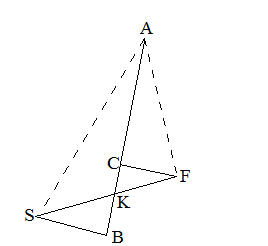
�E�m�}5-15�n
SA�FSK��FA�{SA�FFS
�@
�@
�@
�@
�@
�@
�@
�@
�@
�@
�@
�@
�@�@�@�@
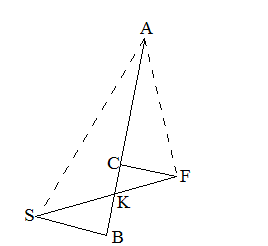
�@�@�@�@�m�}5-15�n��O���i��j
�@
�@A�͕��̂̂���_�ł���B�_S�Ɠ_F�͏œ_�ł���B�����ɂ����āA�O�i�ɂ��ƁA�_A�ł̐ڐ��̐����́A�Q�œ_�ւ̒����̊Ԃ̊p���Q
��������B�䂦�ɁAAK���������A�Q�̐����ASB��AK�AFC��AK�̑��A���ꂼ��A�_B�Ɠ_C���߂�ƁA���p�O�p�`�̑����W����A
�@
�@FK�FSK��FC�FSB�@����@�@
�@FC�FSB��FA�FSA�@����@�A
�@�A�A���A�@FK�FSK��FA�FSA
�䂦�ɁA�@SA�FSK��FA�FFK
����āA�@SA�FSK��FA�{SA�FFS�C�@�@�iFS��FK�{SK�j
�@��V�i�ɂ��ƁA���̔�́A�@��2a�F2e�B�@�i�œ_�ԋ����́A�o�S���̂Q�{������j
�@
�ȉ~�̏œ_���Ɋւ���w�̏ؖ��́A����ɂ��������������A�قǂȂ��j���[�g���̗͊w�A�d�͂̋c�_�ƗZ�������B
�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|
�t�^�F���T�����Љ�i���̂Q�j

�u�}���Y�u��ېV���v(1798-1802)���ҏ㊪�u���S��o���{�v�u��l�ȉ~�o�`�ꕪ�����v���}�̑����y�[�W
�i�w��ېV���x�ʖ{�A����c��w�ÓT�Б����f�[�^�x�[�X���j
�@
�i���j
�@
�����\���ɖ߂�