間重富「垂球精義」の「秘法」

上原　貞治

　

０．はじめに

　江戸時代後期の日本の暦学者、麻田剛立（1734-1799）が1789年頃にケプラーの第３法則を独自に発見した可能性が高いことについては別に論じた（文献1)）。彼の門人の間重富(1756-1815)はこのケプラーの第３法則の根拠を考案しており、その内容は「麻田翁五星距地之奇法」(1795-97頃？）並びに「垂球精義」(1805)に書かれている（文献2,3)）。その大意はケプラーの第３法則と振り子の周期の法則の類似点を指摘したことであるが、間はそれを自然の法則として本質的かつ普遍的なものであると考え、この２つの法則をより接近させた形にして類似性を示そうとした。その試みがここで述解する「垂球精義」の「秘法」部分である。この部分は未完成であるらしく意味が理解できない点が多いが、間のアイデアがどういうものであったか迫ってみたい。

　

１．垂球精義の成立状況

　「垂球精義」は間自身によって書かれた個人的メモのようなもので、直ちに他人に見せることを念頭に書かれたものではない。その概要については文献2)に述べたが、ケプラーの第３法則と振り子の周期の法則を紹介して、その類似点を解説したものである。間は振り子を「垂球」と呼んでいるので、以下では振り子の糸の長さと周期との関係の法則を「垂球の法則」と呼ぶことにする。間は、垂球の法則については中国書「霊台儀象志」（書いたのは南懐仁ことベルギー人フェルビースト）にこれがあり、ケプラーの第３法則についてはこれを麻田剛立が独自に発見した（五星距地之奇法）という。そして、すでに18世紀末、麻田剛立の存命中に２つの法則の類似性について指摘していた（天行方数諸曜帰一理）。垂球精義はこの天行方数諸曜帰一理を中心テーマにしているが、これを書いた時には間はすでにオランダ語本のラランデ暦書にケプラーの第３法則が記載されていたことを知っていた。しかし、彼はニュートンの力学や万有引力の法則については理解していなかったので、その成り立つゆえんについて西洋でどのように考えられていたかは全く知らなかった。　

　

２．垂球精義の内容

　垂球精義の前半では、「垂球の法則」と「五星距地之奇法」（ケプラーの第３法則と同じ）が紹介され、その類似点が論じられる。そのさいに、力のモーメントの釣り合いについても触れられる。その数理を以下に整理する。

　

振り子の糸の長さをr、振動数をn　とすると、垂球の法則は、

　

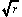
n 〜1/　　　　　　　　　　　　　　　　　　　　　　　 ----- (1)

　

と表される（ここでは　"〜"は異なるr の値を持つ場合に比例関係が成り立つことを示す）。振動数とは単位時間に振り子が往復する回数である。

　一方、ケプラーの第３法則は、惑星の軌道半径をr とし（簡単のために円軌道で近似する）、惑星の公転の角速度をωとすると、角速度と公転周期Tのあいだには、ω=2π/T の関係があるので、

　

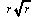
ω 〜 1/（ ）　　　　　　　　　　　　　　　　　　　　　----(2)

　

が成り立つ。ここで、間は、角速度は「視動」（見かけの動き）であるとして、実動である実速度　v = rωを導入し、

　

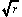
v　〜 1/ 　　　　　　　　　　　　　　　　　　　　　　　----(3)

　

となることを指摘した。そして、(1)式と(3)式が同じ形になることで両者が同じ原理に基づいているとした。これが天行方数諸曜帰一理の最終的な意味であろう。なお、天行方数とは、惑星の公転角速度の平方　ω²　 あるいは　速度の平方　v ²　のことと考えられる。惑星の公転角速度の平均値のことを当時は「平行」と呼んでいた（今日では平均運動と呼んでいる）。

　間は、垂球の法則は力のモーメントの釣り合いと関連しているとした。天秤ばかりの支点からの距離をr 、分銅の重さをmとした場合、釣り合うときに　r　〜1 / m　が成り立つ。ここで、正方形の板状の分銅を考え、分銅の１辺をa とするとmはa ²　に比例するから、結局

　

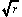
a 〜 1/ 　　　　　　　　　　　　　　　　　　　　　　　　　　----(4)

　

が成り立つ。これは(1)と同形である。全くこじつけであるが、間は、五星距地之奇法と垂球の法則は同じ原理に基づいており、垂球の法則と力のモーメントの釣り合いもまた同じ原理に基づいているという論法から、ケプラーの第３法則は惑星を形成する「気」の密度とその運動の勢いが釣り合った状態として説明できるとした。間は、東洋自然哲学に基づいて天体の運動と地上物体の法則（重さと運動との関係）を統一的に説明しようとしたのである。彼はニュートン力学を知らなかったが、ある意味でニュートンと同じ方向をめざしたのだといえよう。そういう意味で、その気宇壮大さは非常に高く評価されて良いだろう。

　

３．垂球精義の「秘法」のテキスト

　さて、垂球精義の本文最後の５ページに「秘法」として、振り子の運動と惑星の運動を直感的に関連づけるべく、振り子の振動を円運動に焼き直す、というきわめて野心的な試みが成されている。その部分の一部を以下に引用する（原文は漢字と片仮名混じりの文であるが、ここでは読みやすいように平仮名交じりの読み下し文にし、数字も算用数字を使用した。□は判読できなかった部分である。一部推測で補った。括弧内は二行割注。）

　

以下、垂球精義（文献3)）より抜粋

　

秘書 五星運行源理

　（前略。この部分は垂球の法則の計算）

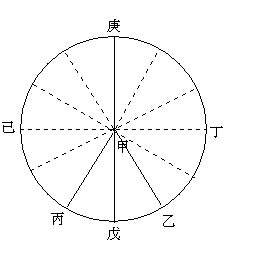
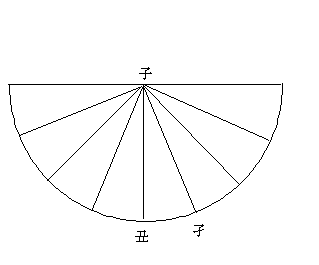
　これより予家法なり。譬えば１日午正より明日午正に至る１周球（垂線１尺）にして100行（100又１万と為すも同じ。又１日を１年に取るもの同じ。又１日に垂線１尺６寸、球およそ６万なるもので１尺と為すもその比例相同じ尺□□なり）とす。乙より戊丙に至る球を１放とす。この球の１日に積もりて100行となる。これを円周とすれば、乙戊丙、又は己庚丁の１周は100行となる。然れば円積を以て□へば、戊甲丙、又は戊甲乙の如きは１球の積なり。又、次の図の如く、垂線４尺、球行１日１周50行（７万とするも700とするも相同じ）、丑子孑を１行とす。円周を積み50行とする。然れば、孑子丑の円積は１行の積なり。唯々、垂球１日１周行、或いは、６万なれば６万を円周に配分するなり。然るにおよそ１日６万万（ママ）は所視の球行なり。垂球の元□に非ず。

（中略。この部分も垂球の法則の計算）

右垂球に因って天度を論ず左の如し。

太陽１周365日有る□は、即ち、１年に365球有る□の如し。故に先ず平行を以て論ぜば、前垂球の例の如く円周に365球を配□するなり。　　（「垂球精義」末尾）

　

（なお、上の「中略」以前の部分に下のような図が２枚ついている）

　

　

　

　

　

　

　

　突飛なアイデアであるにもかかわらず、説明が簡単すぎて何を言おうとしているのかはっきりしないが、以下に間が考えていたことを汲み取ってみたいと思う。

　

４．「秘法」部分の解釈

「中略」以前の部分では、振り子の往復運動の「円周化」がなされる。１周が１日ぶんの振り子の振動による動きになるわけだから、

　

2πr ＝n d　　　　　　　　　　　　　　　　　　　　　　　　　　----(5)

　

となる。ここで、r は振り子の糸の長さ（垂線）で図の円周の半径は糸の長さに対応していると解釈した。n は振動数（１日を単位時間とする）、d は１振動ぶんの移動距離で、振り子の１往復で重りが移動する距離である（すなわち振幅の４倍）。

一方、「中略」以降の部分は、惑星の公転運動の１周を（ここでは地球を例とし、天動説を採って太陽が動くとしている）円周とし、それを周期で分割している。分割された移動距離d は、

　

d ＝2πr / T　　　　　　　　　　　　　　　　　　　　　　　　　----(6)

　

である。以上が垂球精義が提示しているモデルである。垂球精義はここで終わっている。

　(5)式と(6)式が類似しているか調べてみよう。(5)式に、垂球の法則 (1)を適用すると、

　

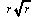
　d 〜r /n　〜 　　　　　　　　　　　　　　　　　　　　　　　　----(5')　

　

となる。振り子の振幅は垂球の法則ではr に関係なく自由にとれるが、単位時間当たりの垂球の移動距離を円周に合わす時は、異なるr に関して(5')の関係が満たされなければならない。

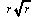
一方、ケプラーの第３法則　T 〜　を(6)式に代入すると、

　

d 〜1/　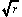　　　　　　　　　　　　　　　　　　　　　　　 　　　----(6')

　

となって、垂球(5')と惑星(6')は同じかたちにならない。間は、これでうまくいくと期待したのだろうがちょっと違ったようである。

　間は次のような計算をするつもりだったのではないかと私は想像する。

　(5')式の右辺がすでに惑星の公転周期の比例に一致している。だから、(6)式でT での割り算を持ち出したのだろうが、(5')式との類似性を考えるならば本当は何か単位時間当たりの運動の量で割り算せねばならなかったはずである。今、(6)式の代わりに全周を速度vで割れば、その商は周期に等しくなり、

　

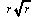
d'　＝2πr / v　＝ T 〜 　　　　　　　　　　　　　　　　　　　　　---(6'')

　

(5')と(6'')は同じかたちとなる。これが間が無意識にめざしていた関係であったかもしれない。しかし、これでも手放しでは喜べない。(5')の左辺 d　は振幅の４倍という「距離」であるが、(6'')式左辺のd' は周期に等しいのだから「時間」なのである。全く違う物理量に類似の比例関係が成り立っていても、それはほとんど意味をなさない。どうやら、間はすでに(5)式の出発点で間違えたようである。

　

５．間はどうするべきだったのか

　ここで、私の考えに従って間の誤りを訂正してみよう。(1)式と(3)式が同型であることを生かすためには、本当は、d = 定数 (r によらない) とするべきだったのである。(5)式で考え方を改めて、全周2πr を定数の１回の振動距離d に分割するならば、垂球は今度は単位時間に円を１周せずに、n d だけ進むことになる。これは垂球の球の平均速度である。全周のこの速度で割ると、垂球の「公転周期」T '　が得られる。 すなわち、

　

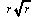
T ' = 2πr / ( nd ) 〜 　　　　　　　　　　　　　　　　　　　　　　---(5'')

これで、(5'')式は(6'')式と同型になった。間は本当はこういう計算をすべきであったのだと考えるが、少なくとも垂球精義の記述の範囲ではこれにたどり着けなかったようである。しかし、こういう図式化を行うまでもなく、(1)式と(3)式の類似性を指摘するだけで彼の論旨としては十分であったと言えるだろう。なお、筆者は、この両式の類似性の力学的根拠について、ニュートン流の運動方程式を用いて文献3)で議論した。

　

６．終わりに

　 間重富の「垂球精義」は、日本人が独自のアイデアに基づいて、天体の運動の根拠を「力学的」かつ数理的に解き明かそうとした希有の書である。特にその秘法部分は、追求が未完であったかあるいは何らかの勘違いのために完成を見なかったようであるが、惑星の運動と振り子の運動の類似性を図の上で明瞭に示そうとしたきわめてユニークな野心作であったと見られる。

　

参考文献

1)　「我が国におけるケプラーの第３法則の受容 ― 麻田剛立の『五星距地之奇法』を中心にして―」上原貞治、天界 Vol. 86, 322-330, 386-390、東亜天文学会、2005;「我が国におけるケプラーの第３法則の受容(�U) ― 麻田剛立『五星距地之奇法』と志筑忠雄『暦象新書』の比較―」上原貞治、天界 Vol.87, 320-328、東亜天文学会、2006.

2)「我が国におけるケプラーの第３法則の受容(�V)」上原貞治、天界 Vol. 88, 67-73、　東亜天文学会、2007.